
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет зубьев на прочность при изгибе
Условие прочностной надежности зуба:
где Для оценки прочностной надежности зубчатой передачи необходимо иметь уравнение, связывающее максимальные напряжения в опасном сечении с внешней нагрузкой на зуб и размерами опасного сечения (параметрами передачи). а). Прямозубые цилиндрические передачи Расчет выполняют для наиболее опасного случая – однопарного зацепления, когда вся внешняя нагрузка передается одной парой зубьев.
где Ft – окружная сила; BW –ширина венца колеса; m –модуль зацепления; yF – коэффициент формы зуба; KFα – коэффициент, учитывающий одновременное участие в передаче нагрузки нескольких пар зубьев (KFα= 1); KFβ –коэффициент концентрации нагрузки; KFυ –коэффициент динамической нагрузки. б). Косозубые цилиндрические передачи
где Ширину зубчатых колес принимают в зависимости от диаметра шестерни. в). Конические передачи В опасном сечении зуба конического колеса максимальные напряжения
где
2. Расчет на контактную прочность активных поверхностей зубьев Расчет зубьев выполняют для фазы зацепления в полюсе.
где Контактные напряжения Для расчета зубчатой передачи на контактную прочность необходимо иметь уравнение, связывающее максимальное напряжение а). Прямозубые и косозубые передачи
где ZH –коэффициент, учитывающий форму сопряженных поверхностей; ZM–коэффициент, учитывающий механические свойства материалов колес (модули упругости Е1 и Е2 и коэффициенты Пуассона,
(21.26)
где
б). Конические передачи (прямозубые) Расчет производить по формуле (21.23), где вместо коэффициента
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.147.4 (0.005 с.) |
 (21.20)
(21.20) –максимальное напряжение в опасном сечении зуба;
–максимальное напряжение в опасном сечении зуба;  – допускаемое напряжение изгиба для материала зуба.
– допускаемое напряжение изгиба для материала зуба. (21.21)
(21.21) (21.22)
(21.22) – коэффициент, учитывающий наклон зубьев;
– коэффициент, учитывающий наклон зубьев;  –коэффициент перекрытия;
–коэффициент перекрытия;  где
где  – коэффициент ширины колеса;
– коэффициент ширины колеса;  для колес низкой твердости (не более 350 НВ);
для колес низкой твердости (не более 350 НВ);  (более 350 НВ).
(более 350 НВ). (21.23)
(21.23) – экспериментальный коэффициент, учитывающий пониженную нагрузочную способность конических передач по сравнению с цилиндрическими передачами из-за конструктивных особенностей; m –модуль в среднем нормальном сечении зуба.
– экспериментальный коэффициент, учитывающий пониженную нагрузочную способность конических передач по сравнению с цилиндрическими передачами из-за конструктивных особенностей; m –модуль в среднем нормальном сечении зуба. 1-1.2 – для передач с круговыми зубьями.
1-1.2 – для передач с круговыми зубьями. (21.24)
(21.24) –максимальное контактное напряжение на активной поверхности зубьев;
–максимальное контактное напряжение на активной поверхности зубьев; 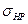 –допускаемое контактное напряжение.
–допускаемое контактное напряжение. (21.25)
(21.25)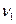 и
и  ). ZM= 275 – для стальных колес; Zε – коэффициент, учитывающий суммарную длину контактных линий.
). ZM= 275 – для стальных колес; Zε – коэффициент, учитывающий суммарную длину контактных линий. – для прямозубых передач.
– для прямозубых передач.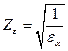 – для косозубых передач.
– для косозубых передач. в предварительных расчетах,
в предварительных расчетах,  –из таблиц;
–из таблиц;  –межосевое расстояние;
–межосевое расстояние;  –ширина колеса; U – передаточное число.
–ширина колеса; U – передаточное число. (21.27)
(21.27) – коэффициент ширины колеса.
– коэффициент ширины колеса. (установлен экспериментально, учитывает особенности прочности конических передач).
(установлен экспериментально, учитывает особенности прочности конических передач).  0,85 –для прямозубых.
0,85 –для прямозубых.


