
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 20. Устойчивость сжатых элементов Конструкций
20.1. Понятие о критической силе для сжатого стержня. Из физики известно, что равновесие тела, устойчиво, если при малом отклонении от равновесного положения возникает сила или пара сил, возвращающая его в положение равновесия. Кроме устойчивого, известны также неустойчивое и безразличное равновесия, но для механических конструкций допустимы лишь случаи устойчивого равновесия. Если по каким-либо причинам упругое тело или конструкция при отклонении от равновесного положения не возвращается к исходному, то говорят, что произошла потеря устойчивости.
Если теперь стержень принудительно выпрямить или, наоборот, изогнуть еще больше, он после нескольких колебаний займет исходное равновесное положение в изогнутом состоянии. Максимальная сжимающая нагрузка
Условие устойчивости сжатого стержня;
Задачу определения критической силы впервые чисто математически решил Л.Эйлер в 1744 г. Формула Эйлера имеет вид
где Экспериментальные исследования, связанные с проверкой формулы Эйлера, показывают, что при прочих равных условиях (одинаковые материал, форма и размеры поперечного сечения, а также длина стержня) значение критической силы зависит от способа закрепления его концов.
Изображены несколько случаев закрепления (рис. 20.3) стержня и указаны соответствующие значения коэффициента приведения 20.2. Критическое напряжение. При осевом нагружении стержня в его поперечных сечениях возникают нормальные напряжения сжатия, которые возрастают по мере увеличения нагрузки. Нормальные напряжения, соответствующие критической силе, называются критическими:
после подстановки значения критической силы из формулы (20.3) получим:
Линейную величину Таким образом,
Безразмерная величина Определяя значение критической силы, Эйлер исходил из рассмотрения упругой линии изогнутого стержня, поэтому формула
справедлива только в пределах применимости закона Гука, иначе говоря, до тех пор, пока критическое напряжение не превышает предела пропорциональности материала стержня, т.е. при условии
Отсюда:
Стоящая в правой части неравенства постоянная для данного материала безразмерная величина называется предельной гибкостью:
Применимость формулы Эйлера определяется условием
Формула Эйлера применима только в тех случаях, когда гибкость стержня больше или равна предельной гибкости того материала, из которого он изготовлен. Как правило, многие конструкции имеют стержни с гибкостью меньше предельной.
|
||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.13.255 (0.006 с.) |
 Явление потери устойчивости упругого тела рассмотрим на примере сжатого стержня. Представим, что на прямолинейный стальной стержень, зажатый одним концом в вертикальном положении (рис. 20.1 а) сверху надет шар. При небольшом значении силы тяжести G 1, сжимающей стержень, он сохраняет прямолинейную форму и находится в устойчивом равновесии.
Явление потери устойчивости упругого тела рассмотрим на примере сжатого стержня. Представим, что на прямолинейный стальной стержень, зажатый одним концом в вертикальном положении (рис. 20.1 а) сверху надет шар. При небольшом значении силы тяжести G 1, сжимающей стержень, он сохраняет прямолинейную форму и находится в устойчивом равновесии. Действительно, если отклонить шар вместе с верхней частью стержня в сторону, то под действием упругих сил стержень, поколебавшись около положения равновесия, снова примет прямолинейную форму. Постепенно увеличивая сжимающую нагрузку путем установки более тяжелых шаров (рис. 20.1 б), увидим, что стержень хотя и сохраняет прямолинейную форму, но при отклонении от положения равновесия возвращается в исходное положение гораздо медленнее. Наконец, при некоторой нагрузке G 3 (рис. 20.1.в) стержень изогнется, и прямолинейная форма устойчивого равновесия переходит в новую, криволинейную форму устойчивого равновесия.
Действительно, если отклонить шар вместе с верхней частью стержня в сторону, то под действием упругих сил стержень, поколебавшись около положения равновесия, снова примет прямолинейную форму. Постепенно увеличивая сжимающую нагрузку путем установки более тяжелых шаров (рис. 20.1 б), увидим, что стержень хотя и сохраняет прямолинейную форму, но при отклонении от положения равновесия возвращается в исходное положение гораздо медленнее. Наконец, при некоторой нагрузке G 3 (рис. 20.1.в) стержень изогнется, и прямолинейная форма устойчивого равновесия переходит в новую, криволинейную форму устойчивого равновесия. , при которой прямолинейная форма стержня устойчива, называется критической силой.
, при которой прямолинейная форма стержня устойчива, называется критической силой. Смысл расчета на устойчивость сжатого стержня заключается в том, чтобы он при некотором значении F осевой нагрузки сохранял устойчивость прямолинейной формы и обладал при этом некоторым запасом устойчивости (рис. 20.2).
Смысл расчета на устойчивость сжатого стержня заключается в том, чтобы он при некотором значении F осевой нагрузки сохранял устойчивость прямолинейной формы и обладал при этом некоторым запасом устойчивости (рис. 20.2). (20.1)
(20.1) (20.2)
(20.2) – коэффициент запаса устойчивости.
– коэффициент запаса устойчивости.
 (20.3)
(20.3) – минимальное значение момента инерции площадки поперечного сечения стержня, так как потеря устойчивости происходит в плоскости наименьшей жесткости;
– минимальное значение момента инерции площадки поперечного сечения стержня, так как потеря устойчивости происходит в плоскости наименьшей жесткости;  –длина стержня.
–длина стержня.
 – коэффициент приведения длины, т.е. число, показывающее, во сколько раз следует увеличить длину шарнирно закрепленного с обоих концов стержня, чтобы критическая сила для него была равна критической силе стержня в данных условиях закрепления.
– коэффициент приведения длины, т.е. число, показывающее, во сколько раз следует увеличить длину шарнирно закрепленного с обоих концов стержня, чтобы критическая сила для него была равна критической силе стержня в данных условиях закрепления. (20.4)
(20.4) (20.5)
(20.5) называют минимальным радиусом инерции сечения.
называют минимальным радиусом инерции сечения. и последняя формула принимает вид
и последняя формула принимает вид или
или 
 называется гибкостью стержня. Она характеризует сопротивляемость стержня потере устойчивости; с увеличением гибкости уменьшается сопротивляемость стержня потере устойчивости. Заметим, что гибкость
называется гибкостью стержня. Она характеризует сопротивляемость стержня потере устойчивости; с увеличением гибкости уменьшается сопротивляемость стержня потере устойчивости. Заметим, что гибкость  . стержня не зависит от материала стержня, а определяется его длиной, формой и размерами сечения.
. стержня не зависит от материала стержня, а определяется его длиной, формой и размерами сечения. (20.6)
(20.6) (20.7)
(20.7)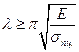
 (20.8)
(20.8) (20.9)
(20.9)


