
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободная и несвободная точки
Материальная точка, движение которой в пространстве не ограничено какими-либо связями, называется свободной. Примером свободной материальной точки может служить искусственный спутник Земли в околоземном пространстве или летящий самолет. Их перемещение в пространстве ничем не ограничено, поэтому летчик на спортивном самолете способен проделывать различные сложные фигуры высшего пилотажа. Задачи динамики сводятся к двум основным: 1) задается закон движения точки, требуется определить действующую на нее силу или систему сил (первая задача динамики); 2) задается система сил, действующая на точку, требуется определить закон движения (вторая задача динамики). Обе задачи динамики решаются с помощью основного закона динамики, записанного в форме Материальная точка, свобода перемещения которой ограничена наложенными связями, называется несвободной. Примером несвободной материальной точки может служить движущийся по рельсам трамвай, если пренебречь его формой и размерами. Для несвободной материальной точки все внешние силы необходимо делить на две категории: активные (движущие) силы и реакции связи (пассивные силы). В связи с этим первая задача динамики несвободной точки сводится к определению реакций связей, если заданы законы движения точки и действующие на нее активные силы. Вторая задача динамики сводится к тому, чтобы, зная действующие на точку активные силы, определить, во-первых, закон движения точки и, во-вторых, реакции связей. Если несвободную материальную точку освободить от связей и заменить связи их реакциями, то движение точки можно рассматривать как свободное, а основному закону динамики придать такой вид:
где Силы инерции Сила, численно равная произведению массы материальной точки на приобретенное ею ускорение и направленная в сторону, противоположную ускорению, называется силой инерции.
Сила инерции в действительности не приложена к получившей ускорение материальной точке, а действует на точку или тело, которое сообщает ускорение этой точке. Поясним это несколькими примерами.
Тяжелый груз, масса которого m, висит на непрочной нити, но способной выдержать натяжение
дополнительная сила инерции При криволинейном движении материальной точки у нее возникает ускорение
и касательная (иначе тангенциальная) сила инерции
Принцип Даламбера Силы инерции широко используются при расчетах и решении технических задач, причем использование сил инерции позволяет свести к знакомым нам уравнениям статики решения многих задач, в которых рассматривается движение несвободной материальной точки.
Прикладывая условно силу инерции Решение задач динамики с помощью принципа Даламбера иногда называют методом кинетостатики. Глава 10. Работа и мощность
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 1753; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.32 (0.007 с.) |
 или
или  .
. ,
, – активные силы;
– активные силы;  – реакции связей; m – масса точки и
– реакции связей; m – масса точки и  – ускорение точки, полученное в результате действия внешних сил (активных и пассивных).
– ускорение точки, полученное в результате действия внешних сил (активных и пассивных). .
.
 . Если теперь резко потянуть нить вертикально вверх, то нить может оборваться. На нить начинает действовать
. Если теперь резко потянуть нить вертикально вверх, то нить может оборваться. На нить начинает действовать
 , численно равная
, численно равная  , выражающая противодействие груза выходу его из состояния инерции. Нить может оборваться и в том случае, если толкнуть в горизонтальном направлении подвешенный груз, заставив его раскачиваться на нити.
, выражающая противодействие груза выходу его из состояния инерции. Нить может оборваться и в том случае, если толкнуть в горизонтальном направлении подвешенный груз, заставив его раскачиваться на нити. (нормальное ускорение) и
(нормальное ускорение) и  (касательное ускорение). Поэтому при криволинейном движении материальной точки возникают две составляющие силы инерции
(касательное ускорение). Поэтому при криволинейном движении материальной точки возникают две составляющие силы инерции  : нормальная (иначе центробежная) сила инерции
: нормальная (иначе центробежная) сила инерции
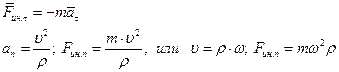


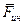 к движущейся материальной точке, можем считать, что активные силы
к движущейся материальной точке, можем считать, что активные силы 


