
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основное уравнение динамики вращающегося тела
Пусть твердое тело под действием внешних сил
называется вращающим моментом.
Рассматривая твердое тело как механическую систему, разобьем его на множество материальных точек с массами Приложим к каждой материальной точке элементарные силы инерции: касательную
(моменты сил У любой точки вращающегося тела числовое значение касательного ускорения
Величина Основное уравнение динамики вращающегося тела:
В СИ момент инерции тела выражается в Кинетическая энергия тела. Кинетический момент Кинетическая энергия тела складывается из кинетических энергий его отдельных точек. 1. При поступательном движении тела скорости всех его точек равны
между собой и равны
где m – масса тела; 2. При вращательном движении тела с некоторой угловой скоростью
все его точки движутся по окружностям различных радиусов
А так как
Кинетическая энергия тела при сложном его движении (при плоскопараллельном, в частности) складывается из кинетической энергии поступательного движения со скоростью центра масс и кинетической энергии вращательного движения с угловой скоростью вокруг оси, проходящей через центр масс, т.е.
Кроме кинетической энергии мерой вращательного движения тела является величина
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.72.53 (0.003 с.) |
 (эти силы на рисунке не показаны) вращается около оси OZ с угловым ускорением
(эти силы на рисунке не показаны) вращается около оси OZ с угловым ускорением 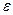 . Алгебраическая сумма моментов всех сил (активных сил и сил сопротивления) относительно оси OZ,
. Алгебраическая сумма моментов всех сил (активных сил и сил сопротивления) относительно оси OZ,

 . Каждая из этих точек движется по окружности радиуса
. Каждая из этих точек движется по окружности радиуса  , с ускорением
, с ускорением  , которое разложим на касательное
, которое разложим на касательное  . и нормальное
. и нормальное  ускорения.
ускорения. и нормальную
и нормальную  . Согласно принципу Даламбера, активные силы, силы реакции связей и силы инерции образуют уравновешенную систему. Поэтому алгебраическая сумма моментов всех этих сил относительно оси OZ должна быть равна нулю, т.е.
. Согласно принципу Даламбера, активные силы, силы реакции связей и силы инерции образуют уравновешенную систему. Поэтому алгебраическая сумма моментов всех этих сил относительно оси OZ должна быть равна нулю, т.е.
 относительно оси OZ равны нулю, т. к. линии действия этих сил пересекают ось).
относительно оси OZ равны нулю, т. к. линии действия этих сил пересекают ось). , поэтому значение
, поэтому значение  , где
, где  – угловое ускорение тела.
– угловое ускорение тела. .
. равная сумме произведений масс всех точек тела на квадраты их расстояний от оси вращения, называется моментом инерции тела (системы) относительно этой оси.
равная сумме произведений масс всех точек тела на квадраты их расстояний от оси вращения, называется моментом инерции тела (системы) относительно этой оси.
 .
.
 – скорости центра масс тела. Поэтому легко понять, что кинетическая энергия тела при поступательном движении
– скорости центра масс тела. Поэтому легко понять, что кинетическая энергия тела при поступательном движении ,
,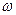
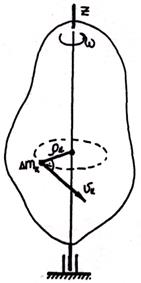
 . Определив кинетическую энергию каждой точки
. Определив кинетическую энергию каждой точки  и сложив ее по всему объему тела, получим:
и сложив ее по всему объему тела, получим:
 – момент инерции тела относительно оси Z, находим для кинетической энергии такое выражение:
– момент инерции тела относительно оси Z, находим для кинетической энергии такое выражение:
 .
. , называемая кинетическим моментом вращающегося тела. Кинетический момент в СИ выражается в
, называемая кинетическим моментом вращающегося тела. Кинетический момент в СИ выражается в  .
.


