
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема об изменении количества движения точки
Пусть на точку массой m действует система постоянных сил, равнодействующая которых
(изменение количества движения точки равно импульсу всех сил). Спроецировав на оси координат обе части векторного равенства (11.2), в общем случае получим: а) систему трех скалярных уравнений:
где б) если силы, действующие на точку, лежат в одной плоскости, то получим два скалярных уравнения; в) если силы действуют вдоль одной прямой, то, спроецировав уравнение (11.2) на эту прямую, получим одно скалярное уравнение:
Теорема об изменении кинетической энергии точки Пусть на точку действует система постоянных сил, равнодействующая которых
На прямолинейном пути
Отсюда с учетом того, что
т.е. изменение кинетической энергии точки равно сумме работ действующих сил. Понятие о механической системе Совокупность материальных точек, связанных между собой силами взаимодействия, называется механической системой. Например, механическую систему образуют Земля и Луна или спортивный самолет и буксируемый им планер. Любое материальное тело рассматривается в механике как механическая система, образуемая совокупностью материальных точек. Абсолютно твердое тело носит название неизменяемой механической системы, так как расстояние между материальными точками остается неизменным. Изменяемые системы – любые машины или механизмы. Если рассматривать какую-либо механическую систему, то силы, действующие на точки системы со стороны точек или тел, не входящих в эту систему, называются внешними (Fe, Re), а силы, действующие на точки системы со стороны точек или тел этой же системы, называются внутренними (Fi).
Главный вектор всех внутренних сил механической системы равен нулю, причем, если рассматриваемая механическая система неизменяемая. Движение механической системы зависит от: 1) действующих сил; 2) суммарной массы системы где m – масса механической системы и 3) положения центра масс системы. Движение центра масс определяется уравнением (только при поступательном движении)
где
Как видим, это уравнение аналогично основному уравнению динамики точки. Смысл его состоит в том, что центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и приложены все внешние силы.
|
|||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.163.58 (0.005 с.) |
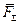 , согласно основному закону динамики равна
, согласно основному закону динамики равна


 .
.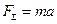 ;
; .
.

 ,
, ,
,
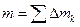 ,
, – массы ее отдельных точек;
– массы ее отдельных точек; ,
, – результирующая всех внешних сил, приложенных к точкам системы; m – масса системы и
– результирующая всех внешних сил, приложенных к точкам системы; m – масса системы и  – ускорение центра масс системы.
– ускорение центра масс системы.


