
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы расчета абсолютного твердого тела как модели механического объектаСтр 1 из 37Следующая ⇒
Оглавление Предисловие.............................................................................................................8 Раздел 1. Основы расчета абсолютного твердого тела как модели механического объекта Глава 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ СТАТИКИ...............................................9 1.1. Общие сведения..........................................................................................9 1.2. Аксиомы статики......................................................................................10 1.3. Связи и их реакции...................................................................................11 Глава 2. Плоская система сходящихся сил...................................14 2.1. Сложение плоской системы сходящихся сил. Геометрическое 2.2. Определение равнодействующей системы сходящихся сил Глава 3. Теория пар сил на плоскости................................................17 3.1. Пара сил. Эквивалентность пар сил........................................................17 3.2. Сложение пар сил. Условие равновесия пар..........................................18 3.3. Момент пары относительно точки...........................................................18 Глава 4. Плоская система произвольно расположенных 4.1. Приведение силы к точке.........................................................................19 4.2. Приведение к точке плоской системы произвольно расположенных сил..............................................................................................................20 4.3. Теорема Вариньона...................................................................................22 4.4. Уравнения равновесия и их различные формы......................................22 4.5. Балочные системы. Разновидности опор и виды нагрузок...................24 4.6. Реальные связи. Трение скольжения и его законы................................25 Глава 5. Пространственная система сил..........................................27 5.1. Сложение пространственной системы сходящихся сил. Условие равновесия.................................................................................................27 5.2. Момент силы относительно оси..............................................................28 5.3. Пространственная система произвольно расположенных сил. Глава 6. Кинематика точки........................................................................31 6.1. Основные понятия кинематики................................................................31 6.2. Способы задания движения точки...........................................................33
6.3. Определение скорости точки при естественном способе задания ее движения....................................................................................................35 6.4. Определение ускорения точки при естественном способе задания ее движения....................................................................................................35 6.5. Частные случаи движения точки.............................................................36 Глава 7. Простейшие движения твердого тела..............................38 7.1. Поступательное движение........................................................................38 7.2. Вращательное движение. Угловая скорость, угловое ускорение.........40 7.3. Частные случаи вращательного движения.............................................41 7.4. Скорости и ускорения различных точек вращающегося тела..............43 7.5. Способы передачи вращательного движения.........................................45 Глава 8. Сложное движение.......................................................................45 8.1. Сложное движение точки.........................................................................45 8.2. Плоскопараллельное движение тела.......................................................47 8.3. Определение скорости любой точки тела при плоскопараллельном движении...................................................................................................48 Глава 9. Движение несвободной материальной точки............50 9.1. Основные понятия и аксиомы динамики................................................50 9.2. Свободная и несвободная точки..............................................................51 9.3. Силы инерции............................................................................................52 9.4. Принцип Даламбера..................................................................................53 Глава 10. Работа и мощность....................................................................53 10.1. Работа постоянной силы на прямолинейном перемещении...............53 10.2. Работа равнодействующей силы............................................................55 10.3. Работа переменной силы на криволинейном пути...............................55 10.4. Мощность.................................................................................................56 10.5. Механический коэффициент полезного действия...............................57 10.6. Работа сил на наклонной плоскости......................................................57 10.7. Работа и мощность при вращательном движении тел.........................59 10.8. Трение качения. Работа при качении тел..............................................60 Глава 11. Общие теоремы динамики.....................................................61
11.1. Импульс силы. Количество движения. Кинетическая энергия...........61 11.2. Теорема об изменении количества движения точки............................61 11.3. Теорема об изменении кинетической энергии точки..........................62 11.4. Понятие о механической системе..........................................................62 11.5. Основное уравнение динамики вращающегося тела...........................63 11.6. Кинетическая энергия тела. Кинетический момент.............................64 Раздел 2. Основы построения и исследования механизмов Глава 12. Структура механизмов...........................................................66 12.1. Основные понятия...................................................................................66 12.2. Классификация кинематических пар. Кинематические цепи.............67 12.3. Структурный синтез и анализ механизмов...........................................68 12.4. Конструктивно-функциональная классификация механизмов...........70 12.5. Передаточное отношение.......................................................................71 Глава 13. Основы расчета и проектирования механизмов....72 13.1. Общие сведения о передачах. Основные виды зубчатых передач.....72 13.2. Общие сведения о методах изготовления зубчатых колес..................74 13.3. Кинематика зубчатых механизмов с неподвижными осями 13.4. Кинематика зубчатых механизмов с подвижными осями Глава 14. Основы кинематического анализа механизмов...77 14.1. Задачи и методы кинематического анализа механизмов. 14.2. Построение положений рычажных механизмов методом засечек.....78 14.3. Определение скоростей и ускорений рычажных механизмов Глава 15. Методические указания к решению задач.................81 15.1. Кинематика зубчатых механизмов с неподвижными осями 15.2. Кинематика зубчатых механизмов с подвижными осями Раздел 3. Раздел 4. Предисловие Это пособие предназначено для студентов, изучающих курс механики по программе, утвержденной Министерством образования Республики Беларусь для высших учебных заведений. В пособии изложение материала, в основном, соответствует традиционной программе механики, исходя из того, что она является комплексной общепрофессиональной дисциплиной по немашиностроительным специальностям. Пособие включает в себя основные положения курсов «Теоретическая механика», «Сопротивление материалов», «Теория механизмов и машин», «Детали машин». Необходимым явилось включение в курс механики в том или ином объеме положений курса «Расчет и конструирование изделий отрасли». Цель пособия – дать студенту знания и навыки по выполнению расчетов и конструированию, необходимые при последующем изучении специальных дисциплин, а также в его профессиональной деятельности. В силу компактности и комплексного характера курса механики, на лекциях требуется лаконичность изложения материала с достаточно полным изложением лишь принципиальных вопросов. Автор использует данный материал при прочтении лекций по механике. Настоящее пособие рекомендуется всем тем, кто изучает, преподает и просто интересуется элементарной механикой.
Пособие предназначено для изучения, повторения и углубления курса механики, а часто и для быстрого нахождения, беглого прочтения и восстановлении в памяти необходимой информации. Пособие может быть использовано для самостоятельной работы студентов. Автор считает своей обязанностью выразить благодарность А.Т.Скойбеде, оказавшему помощь в подготовке книги. Автор будет также благодарен всем товарищам, которые не откажутся в дальнейшем высказать свои замечания об этом пособии. Раздел 1. Основы расчета абсолютного твердого тела
Общие сведения Материальной точкой называют геометрическую точку, обладающую массой. Абсолютно твердым телом называют такое материальное тело, в котором расстояние между любыми двумя точками всегда остается неизменным. Способность тел сопротивляться изменению их формы и размеров называется жесткостью. Мера механического действия одного материального тела на другое называется силой. Сила - величина векторная. Она определяется, во-первых, числовым значением (модулем), во-вторых, точкой приложения (местом контакта взаимодействующих тел), в-третьих, направлением действия. В Международной системе единиц (СИ) сила выражается в ньютонах (сокращенное обозначение Н). 1Н – небольшая сила, поэтому часто употребляют кратные единицы – килоньютон (1 кН = 103 Н) и меганьютон (1 МН = 106 Н). Как всякий вектор, силу можно изобразить графически в виде направленного отрезка.
Сила тяжести всегда направлена вертикально вниз.
Несколько сил, действующих на какое-либо одно твердое тело, называется системой сил. Силы, действующие на твердое тело со стороны других тел, называются внешними. Силы, действующие на материальные точки твердого тела со стороны других точек того же тела, называются внутренними.
Аксиомы статики
Аксиома 1 (принцип инерции). Всякая изолированная материальная точка находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные силы не выведут ее из этого состояния. Состояние покоя или равномерного и прямолинейного движения точки называют равновесием. Аксиома 2 (условие равновесия двух сил). Две силы, приложенные к твердому телу, образуют уравновешенную систему только тогда, когда они равны по модулю и действуют вдоль одной прямой в противоположные стороны.
Аксиома 3 (принцип присоединения и исключения уравновешенных сил). Действие данной системы сил на твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил. Следствие 1. Силу, приложенную к твердому телу, можно переносить вдоль линии ее действия в любую другую точку, действие силы на тело при этом не нарушится. Свойство вектора силы справедливо только в теоретической механике (механике абсолютно твердого тела).
Аксиома 4 (правило параллелограмма). Две приложенные к точке тела силы имеют равнодействующую, приложенную в той же точке и равную диагонали параллелограмма, построенного на этих силах, как на сторонах. Две силы
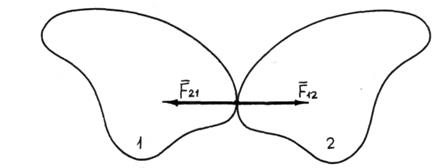
Аксиома 5 (закон действия и противодействия). Силы взаимодействия двух твердых тел друг на друга равны по модулю и направлены по одной прямой в противоположные стороны.
Аксиома 6 (принцип отвердевания). Если деформируемое тело находится в равновесии, то равновесие этого тела не нарушится, если, не изменяя формы, размеров, положения в пространстве, оно превратится в абсолютно твердое тело, т.е. затвердеет.
Связи и их реакции
Твердое тело называется свободным, если оно может перемещаться в пространстве в любом направлении. В качестве примера свободного тела приведем летящий воздушный шар или ракету в космосе. Твердое тело называется несвободным, если его перемещение в пространстве ограничено какими-либо другими телами. Все тела, которые, так или иначе ограничивают перемещение данного тела, называются его связями. Задача определения реакций связей – одна из основных задач статики. Некоторые разновидности связей и правила определения их реакций. 1. Свободное опирание тела о связь. Тело изображено в виде бруска, а связь заштрихована.
2. Гибкая связь. Реакции нитей или цепей всегда направлены вдоль самих связей в сторону от тела к связи.
3. Стержневая связь. Реакции стержневых связей направлены вдоль прямой, проходящей через оси концевых шарниров.
4. Шарнирно-подвижная опора представляет собой видоизменение свободного опирания.
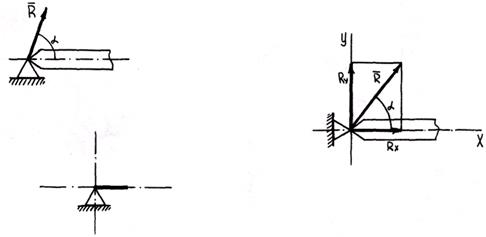
5. Шарнирно-неподвижная опора дает возможность телу свободно поворачиваться около шарнира, но препятствует поступательному перемещению тела в любом направлении, перпендикулярном оси шарнира.
Приведение силы к точке
Теорема о параллельном переносе силы в любую заданную или выбранную точку
Пусть дана сила
Таким образом, всякую силу Операция такого переноса силы называется приведением силы к точке, а появляющаяся при этом пара Операция приведения силы к точке имеет глубокий физический смысл.
Теорема Вариньона
Непосредственно из равенства (
Из последнего рисунка следует, что
т.е. момент равнодействующей ПСПРС относительно любой точки равен алгебраической сумме моментов сил системы, взятых относительно той же точки.
Равномерно распределены.
Равномерно распределенная нагрузка задается двумя параметрами – интенсивностью q, т.е. числом единиц силы (Н или кН), приходящихся на единицу длины (м), и длиной l. В задачах статики, где рассматриваются абсолютно недеформируемые (твердые) балки, равномерно распределенную нагрузку можно заменять равнодействующей сосредоточенной силой
Основные законы трения 1. Сила трения действует в касательной плоскости к поверхностям соприкасающихся тел и при движении направлена против относительного скольжения тела. 2. Статическая сила трения пропорциональна нормальной реакции,
3. Статическая сила трения не зависит от размеров трущихся поверхностей. 4. Статический коэффициент трения ( поверхностей обоих тел и площади их соприкосновения увеличиваются. Следовательно, размеры трущихся поверхностей влияют на статический коэффициент трения, а значит и на силу трения). После начала скольжения тела коэффициент трения несколько уменьшается и принимает значение динамического коэффициента трения f Следовательно,
где
Условие равновесия Ранее подробно изложен процесс приведения сил к точке и доказано, что любая плоская система сил приводится к силе – главному вектору и паре, момент которой называется главным моментом, причем эквивалентные данной системе сил сила и пара действуют в той же плоскости, что и заданная система. Значит, если главный момент изобразить в виде вектора, то главный вектор и главный момент плоской системы сил всегда перпендикулярны друг другу. Рассуждая аналогично, можно последовательно привести к точке силы пространственной системы. Но теперь главный вектор есть замыкающий вектор пространственного (а не плоского) силового многоугольника; главный момент уже нельзя получить алгебраическим сложением моментов данных сил относительно точки приведения. При приведении к точке пространственной системы сил, присоединенные пары действуют в различных плоскостях и их моменты целесообразно представлять в виде векторов и складывать геометрически. Поэтому полученные в результате приведения пространственной системы сил главный вектор (геометрическая сумма сил системы) и главный момент (геометрическая сумма моментов сил относительно точки приведения), вообще говоря, не перпендикулярны друг другу. Векторные равенства Если главный вектор равен нулю, то его проекции на три взаимно перпендикулярные оси также равны нулю. Если главный момент равен нулю, то равны нулю и три его составляющие на те же оси.
Значит, произвольная пространственная система сил статически определима лишь в том случае, когда число неизвестных не превышает шести. Среди задач статики часто встречаются такие, в которых на тело действует пространственная система параллельных друг другу сил.
В пространственной системе параллельных сил неизвестных должно быть не больше трех, иначе задача становится статически неопределимой.
Глава 6. Кинематика точки Основные понятия кинематики
Раздел механики, занимающийся изучением движения материальных тел без учета их масс и действующих на них сил, называется кинематикой. Движение – основная форма существования всего материального мира, покой и равновесие – частные случаи. Всякое движение, и механическое в том числе, происходит в пространстве и во времени. Все тела состоят из материальных точек. Чтобы получить правильное представление о движении тел, начинать изучение нужно с движения точки. Перемещение точки в пространстве выражается в метрах, а также в дольных (см, мм) или кратных (км) единицах длины, время – в секундах. В практике или жизненных ситуациях время часто выражают в минутах или часах. Отсчет времени при рассмотрении того или иного движения точки ведут от определенного, заранее обусловленного начального момента (t = 0). Геометрическое место положений движущейся точки в рассматриваемой системе отсчета называется траекторией. По виду траектории движение точки делится на прямолинейное и криволинейное. Траектория точки может быть определена и задана заранее. Так, например, траектории искусственных спутников Земли и межпланетных станций вычисляют заранее, или если принять движущиеся по городу автобусы за материальные точки, то их траектории (маршруты) также известны. В подобных случаях положение точки в каждый момент времени определяется расстоянием (дуговой координатой) S, т.е. длиной участка траектории, отсчитанной от некоторой ее неподвижной точки, принятой за начало отсчета. Отсчет расстояний от начала траектории можно вести в обе стороны, поэтому отсчет в одну какую-либо сторону условно принимают за положительный, а в противоположную – за отрицательный, т.е. расстояние S – величина алгебраическая. Она может быть положительной (S > 0) или отрицательной (S<0). При движении точка за определенный промежуток времени проходит некоторый путь L, который измеряется вдоль траектории в направлении движения.
Если точка стала двигаться не из начала отсчета O, а из положения, находящегося на начальном расстоянии So то
Векторная величина, характеризующая в каждый данный момент времени направление и быстроту движения точки, называется скоростью.
Скорость точки в любой момент ее движения направлена по касательной к траектории.
Отметим, что это векторное равенство характеризует лишь положение
где Модуль средней скорости равен частному от деления пройденного пути на время, в течение которого этот путь пройден. Векторная величина, характеризующая быстроту изменения направления и числового значения скорости, называется ускорением.
При равномерном движении по криволинейной траектории точка тоже имеет ускорение, так как и в этом случае изменяется направление скорости.
За единицу ускорения принимают обычно
6.2. Способы задания движения точки
Существует три способа: естественный, координатный, векторный. Естественный способ задания движения точки. Если кроме траектории, на которой отмечено начало отсчета O, задана зависимость
между расстоянием S и временем t, это уравнение называется законом движения точки по заданной траектории. Пример:
Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением Координатный способ задания движения точки. Когда траектория точки заранее не известна, положение точки в пространстве определяется тремя координатами: абсциссой X, ординатой Yи аппликатой Z.
Эти уравнения выражают закон движения точки в прямоугольной системе координат (OXYZ). В частном случае, если точка движется в плоскости, закон движения точки выражается двумя уравнениями:
Например. Движение точки в плоской системе координат задано уравнениями Зная закон движения точки в прямоугольной системе координат, можно определить уравнение траектории точки. Например, исключив время t из заданных выше уравнений 6.3. Определение скорости точки при естественном способе Пусть движение точки А по заданной траектории происходит согласно уравнению
За промежуток времени
но оно отличается от значения скорости в момент времени t. Скорость в заданный момент t
т.е. значение скорости точки, движение которой задано естественным способом, в любой момент времени равно первой производной от расстояния (дуговой координаты) по времени. Направление скорости, как отмечалось выше, известно заранее. 6.4. Определение ускорения точки при естественном способе
Вектор
Вектор
равный производной от скорости в данный момент по времени или, иначе, второй производной от расстояния по времени, характеризует быстроту изменения значения скорости. Доказано, что вектор
Значит, модуль нормального ускорения пропорционален второй степени модуля скорости в данный момент, обратно пропорционален радиусу кривизны траектории в данной точке и характеризует быстроту изменения направления скорости.
Модуль ускорения
а направление a (угол
Если векторы
Поступательное движение
Движение твердого тела, при котором любой выбранный в теле отрезок прямой перемещается, оставаясь параллельным своему первоначальному положению, называется поступательным. Рассмотрим две точки А и В, соединенные отрезком АВ. Очевидно, что при перемещении отрезка АВ параллельно первоначальному положению (
параллельным своему первоначальному положению (
Как видим, поступательное движение твердого тела полностью характеризуется движением любой его точки. Обычно поступательное движение тела задается движением его центра тяжести, иначе говоря, при поступательном движении тело можно считать материальной точкой. Примерами поступательного движения тел могут служить какой-либо ползун 1, движущийся в прямолинейных направляющих 2, или прямолинейно движущийся автомобиль (вернее, не весь автомобиль, а его шасси с кузовом). Иногда криволинейное движение на поворотах дорог автомобилей или поездов условно принимают за поступательное. В подобных случаях говорят, что автомобиль или поезд движется с такой-то скоростью или с таким-то ускорением. Примерами криволинейного поступательного движения служат движение вагончика (люльки) подвесной канатной дороги или движение спарника, соединяющего два параллельных кривошипа. В последнем случае каждая точка спарника движется по окружности.
Глава 8. Сложное движение Сложное движение точки Примером сложного движения точки может служить: а) лодка (если ее принять за материальную точку), плывущая от одного берега реки к другому; б) шагающий по ступенькам движущегося эскалатора в метро человек также совершает сложное движение относительно неподвижного свода туннеля. Таким образом, при сложном движении точка, двигаясь относительно некоторой подвижной материальной среды, которую условимся называть подвижной системой отсчета, одновременно передвигается вместе с этой системой отсчета относительно второй системы отсчета, условно принимаемой за неподвижную. Движение некоторой точки М по отношению к подвижной системе отсчета называется относительным. Движение подвижной системы отсчета вместе со всеми связанными с ней точками материальной среды по отношению к неподвижной системе отсчета называется для точки М переносным. Движение точки М по отношению к неподвижной системе отсчета называется сложным, или абсолютным. Для того чтобы видеть сложное (абсолютное) движение точки, наблюдатель должен сам быть связан с неподвижной системой отсчета. Если же наблюдатель находится в подвижной системе отсчета, то он видит лишь относительную часть сложного движения.
Представим, что точка М переместилась за некоторое время относительно подвижной системы координат
Разделим обе части этого равенства на вр
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 324; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.132.194 (0.141 с.) |
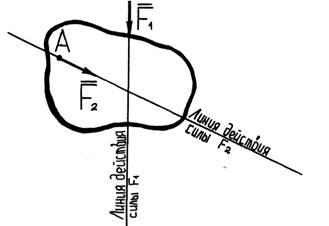




 и
и  приложены к разным точкам тела, но линии их действия лежат в одной плоскости.
приложены к разным точкам тела, но линии их действия лежат в одной плоскости.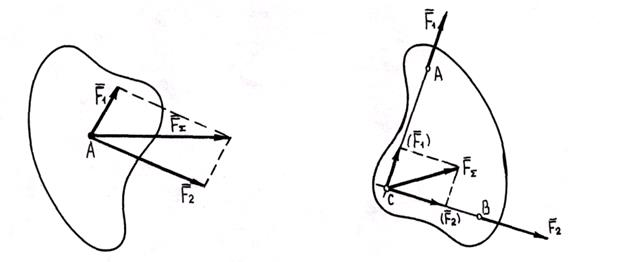




 6. Глухая заделка (жесткое защемление). Исключает любое перемещение тела.
6. Глухая заделка (жесткое защемление). Исключает любое перемещение тела.

 , приложенная к точке А твердого тела, и ее требуется перенести в точку 0. Приложим к телу в точке 0 уравновешенную систему сил
, приложенная к точке А твердого тела, и ее требуется перенести в точку 0. Приложим к телу в точке 0 уравновешенную систему сил  , параллельных
, параллельных  ). Теперь, кроме силы
). Теперь, кроме силы  , приложенной к точке 0, образовались пара сил
, приложенной к точке 0, образовались пара сил  с моментом
с моментом  и момент данной силы
и момент данной силы  т.е.
т.е.  .
. – присоединенной парой.
– присоединенной парой.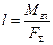 ) вытекает важная зависимость между моментом равнодействующей и моментами составляющих сил, известная в механике как теорема Вариньона. Перепишем предыдущее равенство в таком виде:
) вытекает важная зависимость между моментом равнодействующей и моментами составляющих сил, известная в механике как теорема Вариньона. Перепишем предыдущее равенство в таком виде: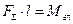
 – момент равнодействующей относительно любой точки, а по формуле
– момент равнодействующей относительно любой точки, а по формуле 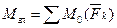 , поэтому последнее равенство можно переписать в виде
, поэтому последнее равенство можно переписать в виде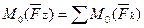 ,
,
 .
.
 )зависит от материала соприкасающихся тел, физического состояния (влажности, температуры, степени загрязнения и т.д.) и качества обработки. (Законы трения относятся к числу не очень точных. Обычно наблюдаются от них значительные отклонения. Например, при увеличении продолжительности неподвижного контакта соприкасающихся тел статический коэффициент трения возрастает, так как в месте контакта постепенно происходит пластическое изменение
)зависит от материала соприкасающихся тел, физического состояния (влажности, температуры, степени загрязнения и т.д.) и качества обработки. (Законы трения относятся к числу не очень точных. Обычно наблюдаются от них значительные отклонения. Например, при увеличении продолжительности неподвижного контакта соприкасающихся тел статический коэффициент трения возрастает, так как в месте контакта постепенно происходит пластическое изменение
 – сила трения скольжения.
– сила трения скольжения. и
и  выражают необходимое и достаточное условие равновесия пространственной системы произвольно расположенных сил.
выражают необходимое и достаточное условие равновесия пространственной системы произвольно расположенных сил.


 .
.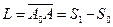




 , а модуль средней скорости за время
, а модуль средней скорости за время  :
: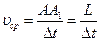
 – путь, пройденный точкой за время
– путь, пройденный точкой за время 

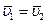

 .
.


 . Тогда в момент времени
. Тогда в момент времени 
 , т.е. точка находится в начале отсчета O; в момент времени
, т.е. точка находится в начале отсчета O; в момент времени  точка находится на расстоянии
точка находится на расстоянии  ; в момент времени
; в момент времени  точка находится на расстоянии
точка находится на расстоянии  от начала отсчета O.
от начала отсчета O.
 или
или  , исключив время.
, исключив время. или
или  .
.
 и
и  (X и Y – см, t – с). Тогда в момент времени
(X и Y – см, t – с). Тогда в момент времени  и
и  , т.е. точка находится в начале координат; в момент времени
, т.е. точка находится в начале координат; в момент времени  ,
,  ; в момент времени
; в момент времени  ,
,  и т.д.
и т.д. . Как видим, в этом случае точка движется по прямой, проходящей через начало координат.
. Как видим, в этом случае точка движется по прямой, проходящей через начало координат.
 точка прошла путь
точка прошла путь  , значение средней скорости на этом пути
, значение средней скорости на этом пути ,
, ,
, – ускорение точки в данный момент – есть геометрическая сумма касательного
– ускорение точки в данный момент – есть геометрическая сумма касательного  и нормального
и нормального  ускорений:
ускорений:
 ,
,

 ,
, ) находим с помощью тригонометрических функций по одной из следующих формул:
) находим с помощью тригонометрических функций по одной из следующих формул: .
. и
и  или
или  ). Если же векторы
). Если же векторы  или
или  ).
). ) точки A и В движутся по одинаковым траекториям, т.е. если траекторию
) точки A и В движутся по одинаковым траекториям, т.е. если траекторию  совместить с траекторией
совместить с траекторией  , то они совпадут. Если вместе с точкой A рассмотреть движение точки C, то при движении тела отрезок АС также остается
, то они совпадут. Если вместе с точкой A рассмотреть движение точки C, то при движении тела отрезок АС также остается
 ) и траектория точки C (кривая
) и траектория точки C (кривая  ) одинакова с траекториями
) одинакова с траекториями  и
и  или
или  , или
, или 
 или
или  , или
, или 


 из начального положения M0 в положение М1 по траектории M0М1 (траектории относительного движения точки). За это же время
из начального положения M0 в положение М1 по траектории M0М1 (траектории относительного движения точки). За это же время 



