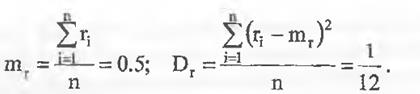Моделирование последовательностей независимых и зависимых случайных испытаний.

В основе метода Монте-Карло лежит генерация случайных чисел, которые должны быть равномерно распределены в интервале (0; 1). Для реализации данно­го метода с использованием компьютера применяют генераторы случайных чисел (ГСЧ).

Если генератор выдает числа, смещенные в какую-то часть интервала (одни числа выпадают чаще других), то результат решения задачи, решаемой статисти­ческим методом, может оказаться неверным. Поэтому проблема использования хорошего генератора действительно случайных и действительно равномерно рас­пределенных чисел стоит очень остро.

Математическое ожидание m_r и дисперсия D_r такой последовательности, со­стоящей из n случайных чисел r_i, должны быть следующими (если это действи­тельно равномерно распределенные случайные числа в интервале от 0 до 1):

Если пользователю потребуется, чтобы случайное число х находилось в ин­тервале (а; b), отличном от (0; 1), нужно воспользоваться формулой х = а + (b - а)r, где г - случайное число из интервала (0; 1). Теперь х - случайное число, рав­номерно распределенное в диапазоне от а до b.

За эталон ГСЧ принят такой генератор, который порождает последователь­ность случайных чисел с равномерным законом распределения в интервале (0; 1). За одно обращение данный генератор возвращает одно случайное число. ГСЧ по способу получения чисел делятся на следующие: физические, табличные, алго­ритмические.

Физические ГСЧ. Примером физических ГСЧ могут служить: монета («орел» - 1, «решка» - 0); игральные кости; поделенный на секторы с цифрами ба­рабан со стрелкой; аппаратурный генератор шума (ГШ), в качестве которого ис­пользуют шумящее тепловое устройство, например, транзистор.

Табличные ГСЧ - в качестве источника случайных чисел используют спе­циальным образом составленные таблицы, содержащие проверенные некоррели­рованные, то есть никак не зависящие друг от друга, цифры. Ниже приведен не­большой фрагмент такой таблицы:

Обходя таблицу слева направо сверху вниз, можно получать равномерно распределенные от 0 до 1 случайные числа с нужным числом знаков после запя­той. Так как цифры в таблице не зависят друг от друга, то таблицу можно обхо­дить разными способами, например сверху вниз или справа налево, или, скажем, можно выбирать цифры, находящиеся на четных позициях.

Достоинство данного метода в том, что он дает действительно случайные числа, так как таблица содержит проверенные некоррелированные цифры. Недос­татки метода: для хранения большого количества цифр требуется много памяти; большие трудности порождения и проверки такого рода таблиц, повторы при ис­пользовании таблицы уже не гарантируют случайности числовой последователь­ности, а значит, и надежности результата.