
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление собственных значений матрицы Методом ДанилевскогоСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сущность метода Данилевского заключается в том, что исходная матрица А:
после
то есть
Вначале нужно строку
Затем вычтем В результате получим матрицу, последняя строка которой имеет желаемый вид 0 0 … 1 0. Произведя те же операции над единичной матрицей, получим матрицу
где
Эти операции равносильны умножению справа матрицы
где
Для подобия матриц нужно умножить полученную матрицу на Очевидно, обратная матрица имеет вид
Обозначим
где
то есть полученная матрица С подобна матрице А. Продолжая этот процесс, получим матрицу Фробениуса.
если все Пример. Привести к виду Фробениуса матрицу:
Решение. Вычисления будем располагать в таблице 4. В строках 1–4 помещаем элементы
Сюда же помещаем элемент В строках 5–8 в графе
Преобразованные элементы третьего столбца получаются с помощью умножения исходных элементов на
Таблица 4
Соответственно, последняя строка матрицы В имеет вид (0 0 1 0). Для контроля пополним матрицу В преобразованными по аналогии элементами:
Полученные результаты записываем в столбце Σ/ . Прибавив к ним элементы третьего столбца, будем иметь контрольные суммы:
Преобразование
Те же преобразования проводим над столбцом Σ:
В результате получаем матрицу С, состоящую из строк 5, 6, Таким образом, матрица Фробениуса имеет вид
Отсюда, решая уравнение 6. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ. Заменим график функции
где Проинтегрировав эту функцию на отрезке
Суммируя полученные выражение по
Оценка погрешности. Для оценки погрешности формулы Симпсона воспользуемся следующей теоремой. Теорема. Пусть функция
Замечание. Если число элементарных отрезков, на которые делится отрезок
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.235.8 (0.011 с.) |


 преобразования подобия приводится к матрице Фробениуса Р:
преобразования подобия приводится к матрице Фробениуса Р: ,
,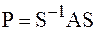 , где
, где  – неособенная матрица. Так как подобные матрицы обладают одинаковыми характеристическими полиномами, то имеем:
– неособенная матрица. Так как подобные матрицы обладают одинаковыми характеристическими полиномами, то имеем: .
. привести в строку
привести в строку  . Предполагая, что
. Предполагая, что  , разделим все элементы
, разделим все элементы  – го столбца матрицы А на
– го столбца матрицы А на  . Тогда её
. Тогда её 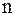 -ая строка примет вид
-ая строка примет вид .
. , из всех остальных ее столбцов.
, из всех остальных ее столбцов. ,
, при
при  . (1)
. (1) . (1')
. (1') на матрицу А.
на матрицу А. , (2)
, (2) при
при  ,
, при
при  . (2')
. (2') слева:
слева:  .
. .
. , то есть
, то есть ,
, (3)
(3) при
при  , (3')
, (3') ,
, .
. данной матрицы и контрольные суммы
данной матрицы и контрольные суммы  в
в  . Элемент
. Элемент  . В строке I записываем элементы третьей строки матрицы
. В строке I записываем элементы третьей строки матрицы  , вычисляемые по формулам (1), (1'):
, вычисляемые по формулам (1), (1'): ,
,  ,
, ,
,  .
. . Число -3,375 должно совпасть с элементами строки I, не входящими в контрольный столбец (после замены элемента
. Число -3,375 должно совпасть с элементами строки I, не входящими в контрольный столбец (после замены элемента  на -1).
на -1). выписываем третью строку матрицы
выписываем третью строку матрицы  , вычисляемые по формулам (2), (2'):
, вычисляемые по формулам (2), (2'):
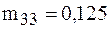 . Например,
. Например,

 8
8



 0,125
-1
0,125
-1

 11,5
11,5
 58,5
58,5



 10
10
 -227,4597
-227,4597






 для строк 5–8 (столбец Σ).
для строк 5–8 (столбец Σ). , произведенное над матрицей В и дающее матрицу
, произведенное над матрицей В и дающее матрицу  , изменяет лишь третью строку матрицы В, то есть седьмую строку таблицы. Элементы строки
, изменяет лишь третью строку матрицы В, то есть седьмую строку таблицы. Элементы строки  получаются по формулам (3), (
получаются по формулам (3), ( ). Например:
). Например: .
. .
. , 8 с контрольными суммами Σ. Далее, приняв матрицу С за исходную и выделив элемент
, 8 с контрольными суммами Σ. Далее, приняв матрицу С за исходную и выделив элемент  , продолжим процесс аналогичным образом.
, продолжим процесс аналогичным образом.
 , найдем собственные значения исходной матрицы.
, найдем собственные значения исходной матрицы. на отрезке
на отрезке  ,
,  ,
,  , параболой, проведенной через точки
, параболой, проведенной через точки  ,
,  , где
, где  – середина отрезка
– середина отрезка  с узлами
с узлами  . Нетрудно убедиться, что уравнение этой параболы имеет вид:
. Нетрудно убедиться, что уравнение этой параболы имеет вид: ,
, .
. .
. , получим квадратурную формулу Симпсона (или формулу парабол):
, получим квадратурную формулу Симпсона (или формулу парабол): .
.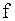 имеет на отрезке
имеет на отрезке  непрерывную производную четвертого порядка
непрерывную производную четвертого порядка  . Тогда для формулы Симпсона справедлива следующая оценка погрешности:
. Тогда для формулы Симпсона справедлива следующая оценка погрешности:  , где
, где .
. , то параболы можно проводить через узлы с целыми индексами, и вместо элементарного отрезка
, то параболы можно проводить через узлы с целыми индексами, и вместо элементарного отрезка  рассматривать отрезок
рассматривать отрезок  длины
длины  . Тогда формула Симпсона примет вид:
. Тогда формула Симпсона примет вид:  , а вместо последней оценки будет справедлива следующая оценка погрешности:
, а вместо последней оценки будет справедлива следующая оценка погрешности: .
.


