
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многочлен Ньютона с конечными разностямиСодержание книги
Поиск на нашем сайте
Рассмотрим случай равноотстоящих узлов интерполяции, т. е. Введем понятие конечных разностей. Пусть известны значения функции в узлах
Эти разности называются разностями первого порядка. Можно составить разности второго порядка:
Аналогично составляются разности k-го порядка:
Выразим конечные разности непосредственно через значение функции:
Таким образом, для любого k можно записать:
Запишем эту формулу для значений разности в узле
Используя конечные разности, можно определить
Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в виде

График многочлена должен проходить через заданные узлы, то есть
Найдем отсюда коэффициенты
Таким образом, для любого
Подставляя эти формулы в выражение многочлена Ньютона, получим его следующий вид:
Полученную формулу можно записать в другом виде. Для этого введем переменную
В этом случае С учетом этих соотношений формулу многочлена Ньютона можно записать в виде
Полученное выражение может аппроксимировать данную функцию
Полученная формула называется первым интерполяционным многочленом Ньютона для интерполяции вперед. Эту интерполяционную формулу обычно используют для вычисления значений функции в точках левой половины рассматриваемого отрезка. Это объясняется следующим: разности Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. В этом случае
Полученная формула называется вторым интерполяционным многочленом назад.
Пример. Используя интерполяционный полином Ньютона, вычислить
Решение. Составляем таблицу конечных разностей.
Для вычисления
Пример. Задана таблица. Найти
При вычислении
При вычислении
Оценим погрешности формул Ньютона вперед и назад:
Формулы приближенного дифференцирования основаны на первой интерполяционной формуле Ньютона. Интерполяционный многочлен Ньютона имеет вид
где Производя перемножение биномов, получим
так как
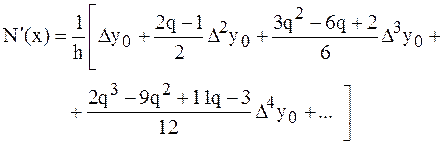
Аналогично можно вычислять производные функции любого порядка. В некоторых случаях требуется находить производные функций
Для производной многочлена Ньютона первого порядка погрешность может быть вычислена по формуле где Пример. Найти Решение.
Здесь Вычисляя погрешность, получим:
Действительно, Таким образом, результаты совпадают до четвертого знака.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.20 (0.007 с.) |

 – называется шагом.
– называется шагом. . Составим разности значений функции:
. Составим разности значений функции:
 .
. .
.

 :
: .
. .
. . Используем эти условия для нахождения коэффициентов многочлена:
. Используем эти условия для нахождения коэффициентов многочлена:
 :
:
 -го коэффициента формула примет вид
-го коэффициента формула примет вид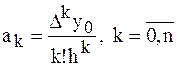 .
.
 .
.
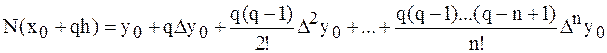 .
. на всем отрезке изменения аргумента
на всем отрезке изменения аргумента 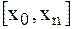 . Однако более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученой формуле) ограничиться случаем
. Однако более целесообразно (с точки зрения повышения точности расчетов и уменьшения числа слагаемых в полученой формуле) ограничиться случаем  , то есть использовать эту формулу для всех
, то есть использовать эту формулу для всех 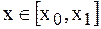 . Для других случаев вместо
. Для других случаев вместо  принять
принять  , если
, если  при
при  . В этом случае интерполяционный многочлен можно записать в виде
. В этом случае интерполяционный многочлен можно записать в виде
 вычисляются через значения функции
вычисляются через значения функции  , причем
, причем  . Из-за этого при больших значениях
. Из-за этого при больших значениях  мы не можем вычислить высших порядков
мы не можем вычислить высших порядков  .
. , то есть
, то есть  , и интерполяционный многочлен Ньютона можно получить в виде:
, и интерполяционный многочлен Ньютона можно получить в виде: .
. , где функция
, где функция 




 тогда
тогда  и
и
 .
.




 положим
положим .
.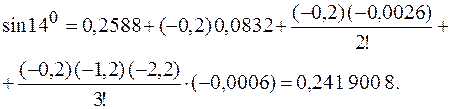
 положим
положим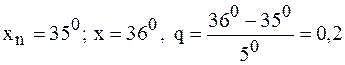 .
.
 где
где  где
где  .
. ,
,

 , то
, то в основных табличных точках
в основных табличных точках  , имеем
, имеем ,
, ,
, функции
функции  , заданной таблично.
, заданной таблично.


 ;
; 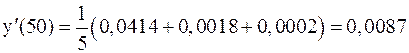 .
. .
. .
.


