Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение нелинейных уравненийСтр 1 из 8Следующая ⇒
ЧИСЛЕННЫЕ МЕТОДЫ Учебное пособие Омск Издательство ОмГТУ УДК 519.61(075) ББК 22.193я73 К 73
Рецензенты: Е. Е. Макаров, к. ф.-м. н. доц., зав. каф «Математическое моделирование» ОмГУ им. Ф.М. Достоевского; Ю. Б. Никитин, к. ф.-м. н., зав. каф. медицинской биологической физики ОмГМА
Котюргина, А.С. К 73 Численные методы: учеб. пособие / А. С. Котюргина. – Омск: Изд-во ISBN 978-5-8149-0898-8
Данное пособие рассматривает основные разделы курса лекций по вычислительной математике, читаемых на потоках ИВТ-2 и Риб-3. В каждой главе содержатся основные теоретические положения, справочный материал, большое количество решенных примеров, иллюстрирующих каждый из рассматриваемых методов, а также наборы задач для индивидуальных заданий. Основными целями издания являются оказание студентам практической помощи в изучении численных методов решения задач алгебры и математического анализа и развитие навыков самостоятельной работы студентов.
Печатается по решению редакционно-издательского совета Омского государственного технического университета
УДК 519.61(075) ББК 22.193я73
ISBN 978-5-8149-0898-8 © ГОУ ВПО «Омский государственный
ВВЕДЕНИЕ Исследование различных явлений или процессов математическими методами осуществляется с помощью математической модели. Математическая модель представляет собой формализованное описание исследуемого объекта посредством систем линейных, нелинейных или дифференциальных уравнений, систем неравенств, определенного интеграла, многочлена с неизвестными коэффициентами и т. д. Математическая модель должна охватывать важнейшие характеристики исследуемого объекта и отражать связи между ними. После того, как математическая модель составлена, переходят к постановке вычислительной задачи. При этом устанавливают, какие характеристики математической модели являются исходными (входными)данными, какие – параметрами модели, а какие – выходными данными. Проводится анализ полученной задачи с точки зрения существования и единственности решения. На следующем этапе выбирается метод решения задачи. Во многих конкретных случаях найти решение задачи в явном виде не представляется возможным, так как оно не выражается через элементарные функции. Такие задачи можно решить лишь приближенно. Под вычислительными (численными) методами подразумеваются приближенные процедуры, позволяющие получать решение в виде конкретных числовых значений. Вычислительные методы, как правило, реализуются на ЭВМ. Для решения одной и той же задачи могут быть использованы различные вычислительные методы, поэтому нужно уметь оценивать качество различных методов и эффективность их применения для данной задачи.
Затем для реализации выбранного вычислительного метода составляется алгоритм и программа для ЭВМ. Современному инженеру важно уметь преобразовать задачу к виду, удобному для реализации на ЭВМ и построить алгоритм решения такой задачи. В настоящее время широко используются как пакеты, реализующие наиболее общие методы решения широкого круга задач (например, Mathcad, Результаты расчета анализируются и интерпретируются. При необходимости корректируются параметры метода, а иногда математическая модель, и начинается новый цикл решения задачи. Пример 3. Применим метод простой итерации для решения системы уравнений
Заметим, что метод простой итерации сходится, так как выполняется условие преобладания диагональных элементов:
Пусть требуемая точность Приведем систему к виду:
Величина Последовательно вычисляем: при
при
при
при
Вычисляем модули разностей значений
При
Вычисляем модули разностей значений
Для сравнения приведем точные значения переменных:
Метод Зейделя Модификацией метода простой итерации можно считать метод Зейделя. В методе простой итерации на
Эти формулы являются расчетными формулами метода Зейделя. Введем нижнюю и верхнюю треугольные матрицы:
Матричная запись расчетных формул (9) имеет вид: Сходимость метода Зейделя. Достаточным условием сходимости метода Зейделя является выполнение неравенства:
Неравенство (10) означает, что для сходимости метода Зейделя достаточно, чтобы любая норма матрицы Если выполнено условие (10), то справедлива следующая оценка погрешности:
где Критерий окончания. Если требуется найти решение с точностью
Метод Зейделя, как правило, сходится быстрее, чем метод простой итерации. Однако возможны ситуации, когда метод простой итерации сходится, а метод Зейделя сходится медленнее или вообще расходится. Пример. Применим метод Зейделя для решения системы уравнений из предыдущего примера. Первые шаги полностью совпадают с процедурой решения по методу простых итераций. Проведем теперь итерации методом Зейделя. При
При вычислении
При вычислении
При вычислении
Аналогичным образом проведем вычисления при Получим: при
при
Известны точные значения переменных:
Сравнение с предыдущим примером показывает, что метод Зейделя сходится быстрее и дает более точный результат.
Постановка задачи Многие практические задачи сводятся к решению системы нелинейных уравнений. Пусть для вычисления неизвестных
В отличие от решения систем линейных алгебраических уравнений (СЛАУ) не существует прямых методов решения систем нелинейных уравнений. Лишь в отдельных случаях эту систему можно решить непосредственно. Например, для случая двух неизвестных иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно другого. В общем случае для решения систем нелинейных уравнений обычно используются итерационные методы. Решение. 1) Начальные приближения можно определить графическим способом. Для этого перепишем систему в виде: Первое из преобразованных уравнений определяет эллипс, а второе – гиперболу. Данная система имеет два решения. Для уточнения выбирают одно из них, принадлежащее области
За начальное приближение принимают
2) Находим
Поскольку Окончательный ответ: Сходимость метода Теорема. Пусть в некоторой замкнутой окрестности Тогда если: 1) функции 2) начальные приближения 3) в неравенства Оценка погрешности
где Сходимость метода считается хорошей, если Пример. Методом итерации решить систему с точностью до
Решение. 1) Приведем систему к форме:
2) Для нахождения начального приближения отделим корни. Построив два графика 3) Проверим приведенную систему на сходимость итерационного процесса:
Следовательно,
4) Для поиска последовательных приближений используют формулы:
Выберем следующие начальные значения:
Поскольку ПРИБЛИЖЕНИЕ ФУНКЦИЙ Метод наименьших квадратов В инженерной деятельности часто возникает необходимость описать в виде функциональной зависимости связь между величинами, заданными таблично или в виде набора точек с координатами
Рис. 12
При аппроксимации желательно получить относительно простую функциональную зависимость (например, многочлен), которая позволила бы «сгладить» экспериментальные погрешности, вычислить значения функции в точках, не содержащихся в исходной таблице. Эта функциональная зависимость должна с достаточной точностью соответствовать исходной табличной зависимости. В качестве критерия точности чаще всего используют критерий наименьших квадратов, т.е. определяют такую функциональную зависимость
Получим систему уравнений
Эту систему уравнений перепишем в следующем виде:
Введем обозначения: Её можно переписать в развернутом виде:
Матричная запись системы имеет следующий вид: Погрешность приближения в соответствии с исходной формулой составит
Линейная аппроксимация
Отсюда система для нахождения коэффициентов
Её можно решить методом Крамера. Квадратичная аппроксимация
Или в развёрнутом виде
Решение системы уравнений Пример. Построим по методу наименьших квадратов многочлены первой и второй степени и оценим степень приближения. Значения
Вычислим коэффициенты Для линейной аппроксимации система уравнений определения коэффициентов
Решая эту систему, получим:
Для квадратичной аппроксимации система уравнений определения коэффициентов
И коэффициенты равны:
Сравним значения, рассчитанные для функциональной зависимости, с исходными данными. Результаты приведены в табл. 3. Таблица 3
Погрешность приближения в соответствии с исходными формулами составит:
Многочлен Лагранжа Будем искать многочлен в виде линейной комбинации множеств степени При этом потребуем, чтобы каждый многочлен
Действительно,
Подставив эти формулы в исходный многочлен, получим:
Эта формула называется интерполяционным многочленом Лагранжа. Пример. Построить интерполяционный многочлен Лагранжа
Решение. Составим таблицу
Подставляя эти значения в формулу Лагранжа, получим:
Если функция
где
Решение.
Здесь Вычисляя погрешность, получим:
Действительно, Таким образом, результаты совпадают до четвертого знака. Постановка задачи Коши Известно, что обыкновенное дифференциальное уравнение первого порядка имеет вид: Решением этого уравнения является дифференцируемая функция
Рис. 13
Производную Исходное уравнение определяет целое семейство решений. Чтобы выделить одно решение, задают начальное условие: Задача Коши заключается в отыскании функции Теорема. Пусть функция Даже для простых дифференциальных уравнений первого порядка не всегда удается получить аналитическое решение. Поэтому большое значение имеют численные методы решения. Численные методы позволяют определить приближенные значения искомого решения Численные методы не позволяют найти решение в общем виде, зато они применимы к широкому классу дифференциальных уравнений. Сходимость численных методов решения задачи Коши. Пусть Численный метод решения задачи Коши называется сходящимся, если для него Метод Эйлера Простейшим методом решения задачи Коши является метод Эйлера. Будем решать задачу Коши
на отрезке Эти формулы и начальное условие являются расчетными формулами метода Эйлера. Геометрическая интерпретация одного шага метода Эйлера заключается в том, что решение на отрезке Оценка погрешности. Для оценки погрешности метода Эйлера воспользуемся следующей теоремой. Теорема. Пусть функция
Тогда для метода Эйлера справедлива следующая оценка погрешности: Оценка погрешности метода Эйлера часто бывает затруднительна, так как требует вычисления производных функции
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 507; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.150.89 (0.152 с.) |
 технический университет», 2010
технический университет», 2010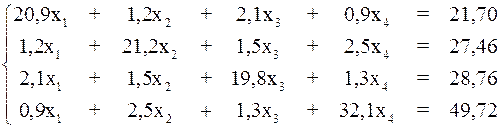 .
.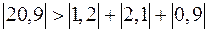 ,
,  ,
,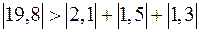 ,
, 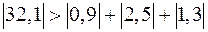 .
. . Вычисления будем проводить с четырьмя знаками после десятичной точки.
. Вычисления будем проводить с четырьмя знаками после десятичной точки.
 равна 0,1179, т. е. выполняется условие
равна 0,1179, т. е. выполняется условие  и можно пользоваться критерием окончания итерационного процесса (8). В качестве начального приближения возьмем элементы столбца свободных членов:
и можно пользоваться критерием окончания итерационного процесса (8). В качестве начального приближения возьмем элементы столбца свободных членов:  . Вычисления будем вести до тех пор, пока все величины
. Вычисления будем вести до тех пор, пока все величины  ,
,  , а следовательно, и
, а следовательно, и 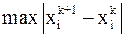 не станут меньше
не станут меньше  .
.





 .
.
 .
.
 .
.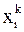 при
при  и
и  :
: . Так как все они больше заданной точности
. Так как все они больше заданной точности  , продолжаем итерации.
, продолжаем итерации.
 .
. . Все они меньше заданной точности
. Все они меньше заданной точности  , поэтому итерации заканчиваем. Приближенным решением системы являются следующие значения:
, поэтому итерации заканчиваем. Приближенным решением системы являются следующие значения: .
.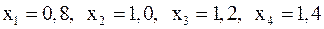 .
. -ой итерации значения
-ой итерации значения  ,
,  вычисляются подстановкой в правую часть (6) вычисленных на предыдущей итерации значений. В методе Зейделя при вычислении
вычисляются подстановкой в правую часть (6) вычисленных на предыдущей итерации значений. В методе Зейделя при вычислении  ,
, 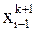 , уже найденные на
, уже найденные на  , …,
, …,  , как в методе простой итерации, т.е.
, как в методе простой итерации, т.е.  (9)
(9) и
и  .
. . Так как
. Так как  , точное решение
, точное решение  исходной системы удовлетворяет равенству:
исходной системы удовлетворяет равенству: 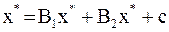 .
.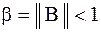 . (10)
. (10) был меньше единицы.
был меньше единицы. , (11)
, (11) – норма матрицы
– норма матрицы  , итерационный процесс следует закончить, как только на
, итерационный процесс следует закончить, как только на 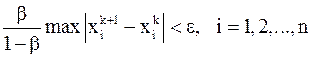 . Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство
. Поэтому в качестве критерия окончания итерационного процесса можно использовать неравенство 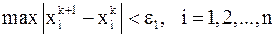 , где
, где 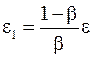 . Если выполняется условие
. Если выполняется условие , то можно пользоваться более простым критерием окончания:
, то можно пользоваться более простым критерием окончания: .
.
 .
. используем уже полученное значение
используем уже полученное значение  :
: .
. используем уже полученные значения и
используем уже полученные значения и  .
. используем уже полученные значения
используем уже полученные значения  .
. и
и 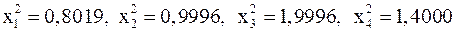 .
. .
. требуется решить систему
требуется решить систему 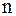 нелинейных уравнений:
нелинейных уравнений: , иначе
, иначе  .
.
 и
и  .
. и
и  .
.








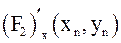

 , то
, то  .
.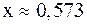 и
и  .
. имеется одно и только одно решение
имеется одно и только одно решение  и
и  приведенной системы.
приведенной системы. и
и 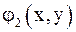 определены и непрерывно дифференцируемы в
определены и непрерывно дифференцируемы в  ;
; ,
, 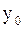 и все последующие приближения
и все последующие приближения  принадлежат
принадлежат  или
или , то процесс последовательных приближений сходится к решению
, то процесс последовательных приближений сходится к решению  ,
,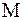 – наибольшее из чисел
– наибольшее из чисел  и
и  , входящих в эти неравенства.
, входящих в эти неравенства. ; при этом
; при этом 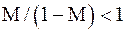 . Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001.
. Поэтому если в двух последовательных приближениях совпадают, например, три десятичных знака после запятой, то ошибка последнего приближения не превосходит 0,001. .
.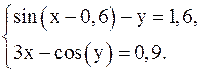

 и
и  и найдя их точку пересечения, можно увидеть, что система имеет единственное решение, заключенное в области
и найдя их точку пересечения, можно увидеть, что система имеет единственное решение, заключенное в области  и
и 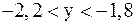 .
.
 и
и  т.е. условия сходимости выполняются.
т.е. условия сходимости выполняются.
 .
. , то
, то  и
и  .
. , где
, где 
 , при которой
, при которой  обращается в минимум. Погрешность приближения оценивается величиной
обращается в минимум. Погрешность приближения оценивается величиной 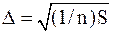 . В качестве функциональной зависимости рассмотрим многочлен
. В качестве функциональной зависимости рассмотрим многочлен 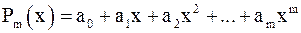 . Формула минимизируемой функции примет вид
. Формула минимизируемой функции примет вид  . Условия минимума
. Условия минимума  можно записать, приравнивая нулю частные производные
можно записать, приравнивая нулю частные производные  .
. или
или  ,
,  .
. ,
,  . Последняя система может быть записана так:
. Последняя система может быть записана так:  ,
,  .
. . Для определения коэффициентов
. Для определения коэффициентов  , и, следовательно, искомого многочлена, необходимо вычислить суммы
, и, следовательно, искомого многочлена, необходимо вычислить суммы  и решить последнюю систему уравнений. Матрица
и решить последнюю систему уравнений. Матрица  этой системы является симметричной и положительно определенной.
этой системы является симметричной и положительно определенной. . Рассмотрим частные случаи
. Рассмотрим частные случаи  и
и  .
. .
. .
. ;
; 
 ,
,  .
. имеет вид:
имеет вид: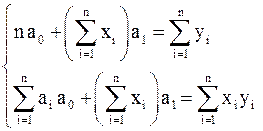 .
. .
. .
.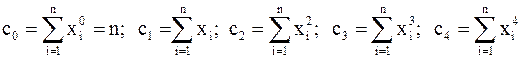 .
. .
. ,
,  .
.
 в точках
в точках  ,
,  приведены в следующей таблице.
приведены в следующей таблице.
 по формулам для линейной и квадратичной аппроксимация
по формулам для линейной и квадратичной аппроксимация 

 ;
;  .
. и
и  многочлена первой степени
многочлена первой степени  имеет вид:
имеет вид: .
.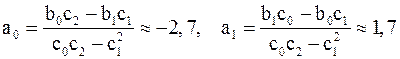 .
.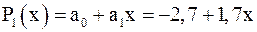 .
. и
и  многочлена второй степени
многочлена второй степени  .
.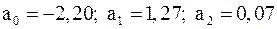 . Тогда
. Тогда .
.

 .
. .
. :
: 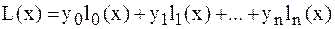 .
.
 во всех узлах интерполяции, за исключением одного
во всех узлах интерполяции, за исключением одного  , где он равен 1. Легко проверить, что этим условиям отвечает многочлен вида
, где он равен 1. Легко проверить, что этим условиям отвечает многочлен вида .
. . При
. При  числитель выражения равен 0. По аналогии получим:
числитель выражения равен 0. По аналогии получим: ,
, .
. .
. , совпадающий с функцией
, совпадающий с функцией  в точках
в точках 
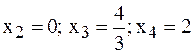 .
.

 непрерывно дифференцируема до
непрерывно дифференцируема до 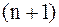 -го порядка включительно, то остаточный член интерполяционного многочлена в форме Лагранжа имеет вид
-го порядка включительно, то остаточный член интерполяционного многочлена в форме Лагранжа имеет вид ,
, – внутренняя точка минимального отрезка, содержащего узлы интерполирования
– внутренняя точка минимального отрезка, содержащего узлы интерполирования 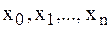 и точку
и точку 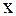 .
.


 ;
;  .
. .
. .
.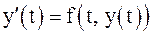 .
. , которая при подстановке в уравнение обращает его в тождество. На рис. 13 приведен график решения исходного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.
, которая при подстановке в уравнение обращает его в тождество. На рис. 13 приведен график решения исходного дифференциального уравнения. График решения дифференциального уравнения называется интегральной кривой.
 в каждой точке
в каждой точке 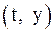 можно геометрически интерпретировать как тангенс угла
можно геометрически интерпретировать как тангенс угла  наклона касательной к графику решения, проходящего через эту точку, т е.:
наклона касательной к графику решения, проходящего через эту точку, т е.:  .
. , где
, где  – некоторое заданное значение аргумента
– некоторое заданное значение аргумента  , а
, а  , удовлетворяющей исходному уравнению и начальному условию. Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения
, удовлетворяющей исходному уравнению и начальному условию. Обычно определяют решение задачи Коши на отрезке, расположенном справа от начального значения 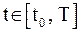 . Разрешимость задачи Коши определяет следующая теорема.
. Разрешимость задачи Коши определяет следующая теорема.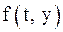 определена и непрерывна при
определена и непрерывна при 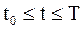 ,
, 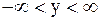 и удовлетворяет условию Липшица:
и удовлетворяет условию Липшица:  , где
, где  некоторая постоянная, а
некоторая постоянная, а  – произвольные значения. Тогда для каждого начального значения
– произвольные значения. Тогда для каждого начального значения  . Точки
. Точки 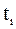 называются узлами сетки, а величина
называются узлами сетки, а величина  – шагом сетки. Часто рассматривают равномерныесетки, для которых шаг
– шагом сетки. Часто рассматривают равномерныесетки, для которых шаг 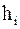 постоянен,
постоянен,  . При этом решение получается в виде таблицы, в которой каждому узлу сетки
. При этом решение получается в виде таблицы, в которой каждому узлу сетки 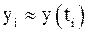 .
. , заданную в узлах сетки
, заданную в узлах сетки 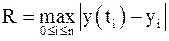 .
. при
при  . Говорят, что метод имеет
. Говорят, что метод имеет 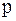 -ый порядок точности, если для погрешности справедлива оценка
-ый порядок точности, если для погрешности справедлива оценка 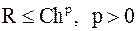 ,
, 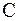 – константа,
– константа, 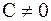 .
.
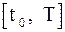 . Выберем шаг
. Выберем шаг  и построим сетку с системой узлов
и построим сетку с системой узлов  . В методе Эйлера вычисляются приближенные значения функции
. В методе Эйлера вычисляются приближенные значения функции 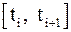 ,
, 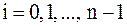 , получим приближенное равенство:
, получим приближенное равенство:  ,
,  ,
,  , проведенной в точке
, проведенной в точке 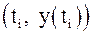 к интегральной кривой, проходящей через эту точку. После выполнения
к интегральной кривой, проходящей через эту точку. После выполнения 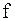 удовлетворяет условиям:
удовлетворяет условиям: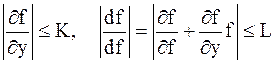 .
. , где
, где  – длина отрезка
– длина отрезка 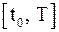 . Мы видим, что метод Эйлера имеет первый порядок точности.
. Мы видим, что метод Эйлера имеет первый порядок точности.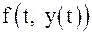 . Грубую оценку погрешности дает правило Рунге (правило двойного пересчета), которое используется для различных одношаговых методов, имеющих
. Грубую оценку погрешности дает правило Рунге (правило двойного пересчета), которое используется для различных одношаговых методов, имеющих 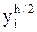 – приближения, полученные с шагом
– приближения, полученные с шагом 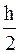 , а
, а 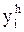 – приближения, полученные с шагом
– приближения, полученные с шагом  . Тогда справедливо приближенное равенство:
. Тогда справедливо приближенное равенство: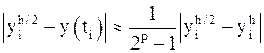 .
.