
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изменение энтропии при нагревании (охлаждении).Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Второй закон термодинамики в дифференциальной форме:
Применим уравнение к изобарному процессу (р = const). Для 1 моль вещества
При нагревании вещества от температуры Т 1 до температуры Т 2 изменение энтропии равно:
Зависимость Ср от температуры выражается уравнением
Тогда
После интегрирования получим:
При V = const:
Тогда
Изменение энтропии в ходе химической реакции, протекающей при Так как энтропия – функция состояния, то ее изменение в ходе химической реакции можно рассчитать по уравнению:
где Sj, Si – энтропии продуктов реакции и исходных веществ соответственно при температуре реакции; nj, ni – стехиометрические коэффициенты. Если реакция протекает при температуре, отличной от 298 К, то энтропию вещества рассчитывают по уравнению (1.22), приняв для удобства за Т 1 температуру 298, а за Т 2 – температуру реакции:
где D S – изменение энтропии вещества при изменении температуры от 298 К до Т. Тогда с учетом уравнения (1.23) получим:
где
Абсолютные значения энтропии твердых, жидких И газообразных тел Абсолютное значение энтропии твердых кристаллических тел. Воспользуемся для расчета энтропии кристаллического тела уравнением II закона термодинамики:
Проинтегрируем уравнение в неопределенных пределах от абсолютного нуля до температуры Т:
Для расчета Немецкий ученый Планк сформулировал постулат, в соответствии с которым: энтропия идеальной конденсированной системы вблизи абсолютного нуля равна нулю: Идеальная конденсированная система – твердое тело, в кристаллической решетке которого нет дефектов, и наблюдается абсолютный порядок. Термодинамическая вероятность идеального кристалла равна единице, а энтропия равна нулю:
Постулат Планка иногда называют III началом термодинамики. Тогда появляется возможность рассчитать абсолютные значения энтропии твердых веществ при любой температуре:
Абсолютное значение энтропии жидкости. Абсолютное значение энтропии жидкости при температуре Т равно:
где
Подставляем выражения для Δ Sтв, Δ Sпл и Δ Sж:
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 888; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.62.46 (0.01 с.) |


 ;
; .
. . (1.22)
. (1.22) ,
, .
. .
. ,
,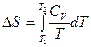 .
. , (1.23)
, (1.23) ,
, ,
, и т.д.
и т.д.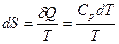 .
. ,
, .
. необходимо знать зависимость
необходимо знать зависимость  , а также
, а также  , то есть энтропию твердого кристаллического тела при абсолютном нуле.
, то есть энтропию твердого кристаллического тела при абсолютном нуле. .
.
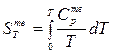 .
. ,
, – изменение энтропии кристаллического вещества в интервале температур от абсолютного нуля до температуры плавления Т пл (численно равно абсолютному значению энтропии твердого вещества при Т пл:
– изменение энтропии кристаллического вещества в интервале температур от абсолютного нуля до температуры плавления Т пл (численно равно абсолютному значению энтропии твердого вещества при Т пл:  ); Δ Sпл – изменение энтропии при плавлении твердого кристаллического вещества; Δ Sж . – изменение энтропии при нагревании жидкости от Т пл. до температуры Т.
); Δ Sпл – изменение энтропии при плавлении твердого кристаллического вещества; Δ Sж . – изменение энтропии при нагревании жидкости от Т пл. до температуры Т. .
.


