
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Самопроизвольных процессов в изолированных системахСодержание книги
Поиск на нашем сайте
В самопроизвольных (необратимых) процессах возможно множество вариантов перехода системы из начального в конечное состояние. Обратимо процесс можно провести только одним путем. Во всех случаях к системе применим I закон термодинамики, согласно которому полное количество энергии в системе должно сохраняться в любом процессе: Q = D U + A, но распределение энергии зависит от характера процесса. В случае обратимых процессов Q обр.= T D S и A = A max. Поэтому I закон термодинамики для обратимых и необратимых процессов принимает следующий вид: T D S = D U + A max, Qн/о = D U + Aн/о. Вычитая почленно из первого равенства второе, получим T D S - Qн/о = A max - Aн/о. Так как внутренняя энергия U – функция состояния, ее изменение одинаково в обратимых и необратимых процессах. Учитывая, что Aн/о < A max, приходим к выводу, что T D S - Qн/о > 0,
Неравенство (1.20) – математическое выражение II закона термодинамики для необратимых процессов. В общем виде II закон термодинамики записывается
Знак «=» относится к обратимым процессам, «>» – к необратимым. Необходимо отметить, что изменение энтропии одинаково как при обратимом, так и при необратимом процессах, но во втором случае теплоприемник получит больше теплоты (при одинаковых значениях теплоты, отданной нагревателем), чем в обратимом цикле, происходит большее обесценивание энергии, т.е. переход энергии в состояние, не способное производить работу.
В изолированных системах в случае необратимых процессов каждое последующее состояние системы отличается от предыдущего бóльшим значением энтропии. Каждое последующее состояние в самопроизвольных процессах обладает большей вероятностью, чем предыдущее.
В изолированной системе по мере переноса тепла от нагревателя к теплоприемнику разность температур Т 1 и Т 2 уменьшается в течение всего времени, когда совершается работа. Это означает, что количество энергии, которое может быть потрачено на работу (зависит от разности температур), должно все время уменьшаться. Наоборот, количество энергии, которое уже невозможно превратить в работу, т.е. количество связанной энергии, должно возрастать. Это увеличение недоступной для нас энергии есть следствие II закона термодинамики: в любом самопроизвольном процессе количество недоступной энергии увеличивается со временем.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 226; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.116 (0.009 с.) |

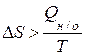 . (1.20)
. (1.20) ,
, .
. В изолированных системах отсутствует подвод теплоты из внешней среды (Q = 0), поэтому в изолированной системе энтропия либо остается постоянной в состоянии равновесия, либо возрастает при необратимом (самопроизвольном) течении процесса. Рост энтропии продолжается до установления равновесного состояния, при этом значение энтропии максимально (рис. 1.6).
В изолированных системах отсутствует подвод теплоты из внешней среды (Q = 0), поэтому в изолированной системе энтропия либо остается постоянной в состоянии равновесия, либо возрастает при необратимом (самопроизвольном) течении процесса. Рост энтропии продолжается до установления равновесного состояния, при этом значение энтропии максимально (рис. 1.6).


