
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о теплоемкости веществСодержание книги
Поиск на нашем сайте
Теплоемкостьсистемы(или тела) – это отношение количества сообщенной системе теплоты к наблюдаемому при этом повышению температуры (при отсутствии химической реакции, переходов вещества из одного агрегатного состояния в другое). Теплоемкость пропорциональна количеству вещества. Различают удельную и молярную теплоемкость. Удельная теплоемкость Суд – это количество теплоты, необходимое для нагревания единицы массы вещества на 1 К. Единица измерения удельной теплоемкости – Дж/(г×К). Молярная теплоемкость С – это количество теплоты, необходимое для нагревания 1 моль вещества на 1 К. Единица измерения молярной теплоемкости – Дж/(моль×К). Молярная и удельная теплоемкости связаны соотношением:
где М – молярная масса. Различают среднюю и истинную теплоемкости. Средняя теплоемкость
Истинная теплоемкость С соответствует бесконечно малому изменению температуры:
Легко установить связь между средней и истинной теплоемкостями, интегрируя (1.8) в интервале температур от Т 1 до Т 2 и подставляя полученное выражение для Q в (1.7):
В зависимости от условий, при которых производится нагревание, различают теплоемкость при постоянном объеме СV (изохорную теплоемкость) и теплоемкость при постоянном давлении Cp (изобарную теплоемкость):
Если нагревание осуществляется при V = const, вся теплота идет на увеличение внутренней энергии; при p = const кроме увеличения внутренней энергии совершается работа расширения. Если постоянство объема или давления оговаривается, частную производную в (1.9) заменяют полной:
Интегрируя выражения (1.10) в интервале температур от Т 1 до Т 2, и принимая, что Cp и СV в указанном интервале температур постоянны, получим:
Установим взаимосвязь между Cp и СV для 1 моль идеального газа. В соответствии с уравнением Менделеева-Клапейрона (1.1) pV = RT. Тогда
Таким образом,
Изобарная и изохорная теплоемкости идеального газа отличаются на величину универсальной газовой постоянной R. Для одноатомного идеального газа
Для двухатомного идеального газа при средних температурах
Изобарная и изохорная теплоемкости твердых веществ практически равны. Теплоемкость твердых, жидких и газообразных тел зависит от температуры. Наиболее часто зависимость теплоемкости индивидуальных веществ от температуры выражается эмпирическим уравнением вида:
где a, b, c, c ’ – эмпирические коэффициенты, вычисленные на основе экспериментальных данных. Для органических веществ коэффициент c ’ = 0, для неорганических – c = 0. Данное эмпирическое уравнение применимо только в определенном интервале температур. Поэтому коэффициенты a, b, c и c’ не имеют физического смысла. Для многих веществ они приведены в справочниках (с указанием температурного интервала, в котором их можно использовать). 1.3.3 Влияние температуры на тепловой эффект химической реакции. Уравнение Кирхгофа Температура оказывает большое влияние на тепловые эффекты химических реакций. Поставим задачу количественно охарактеризовать это влияние. Рассмотрим химическую реакцию, протекающую при р = const:
Пусть энтальпия исходных веществ, участвующих в реакции равна Н 1, а энтальпия продуктов реакции – Н 2. Тогда
где
Аналогично, для продуктов реакции:
Вычитая почленно из уравнения (1.13) уравнение (1.12), получим:
где Для химической реакции
Аналогично для процессов, протекающих при V = const,
Для химической реакции
Полученные уравнения (1.13), (1.14) выражают закон Кирхгофа: Температурный коэффициент теплого эффекта химической реакции (или других процессов), протекающих при р = const или V = const равен разности теплоемкостей системы в исходном и конечном состоянии. Проанализируем уравнения Кирхгофа. Из уравнений следует, что влияние температуры на тепловой эффект обусловливается знаком величины – если Δ Ср > 0, то производная – если Δ Ср < 0, то производная – если Δ Ср = 0, то тепловой эффект реакции не зависит от температуры. Закон Кирхгофа позволяет рассчитывать тепловые эффекты реакции при любой температуре. Получим уравнение для расчета теплового эффекта, протекающего при
При интегрировании уравнения Кирхгофа часто используется температурная зависимость теплоемкости в виде степенных рядов, которые справедливы в определенном температурном интервале. Чаще всего интегрирование проводят в определенных пределах, приняв за нижний предел интегрирования температуру 298 К, а за верхний – температуру Т. Тепловой эффект реакции при 298 К можно легко рассчитать, используя первое или второе следствия из закона Гесса. В результате интегрирования получим:
Так как изобарная теплоемкость обладает свойствами функции состояния, для Δ Ср можно записать:
где
Подставив выражение для Δ Ср в (1.15) и проинтегрировав, получим:
Если в интервале температур от 298 К до Т одно из реагирующих веществ претерпевает изменение агрегатного состояния, то есть происходит фазовое превращение, то интервал температур разбивается на два интервала: от 298 К до Т ф.п. (температура, при которой происходит фазовый переход) и от Т ф.п. до Т:
Вычисление теплового эффекта по уравнению Кирхгофа значительно упрощается, если воспользоваться средними теплоемкостями Тогда
где Приведем уравнение (1.16) к виду
Выражение, заключенное в скобки, всегда постоянно, таким образом, в данном случае зависимость теплового эффекта от температуры является линейной. Недостаток данного метода расчета тепловых эффектов заключается в его невысокой точности.
|
||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.008 с.) |

 ,
,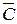 определяется отношением сообщенной системе теплоты к наблюдаемому при этом повышению температуры:
определяется отношением сообщенной системе теплоты к наблюдаемому при этом повышению температуры: . (1.7)
. (1.7) . (1.8)
. (1.8)
 (1.9)
(1.9) (1.10)
(1.10)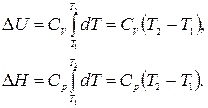
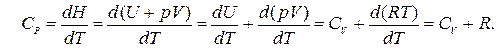
 .
.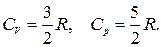 .
.
 , (1.11)
, (1.11) .
.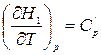 , (1.12)
, (1.12) – теплоемкость системы в исходном состоянии:
– теплоемкость системы в исходном состоянии: .
.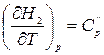 , (1.13)
, (1.13) .
. ,
, .
. равно
равно .
. ,
, ,
, . (1.14)
. (1.14) .
. :
: , следовательно, с повышением температуры тепловой эффект реакции будет возрастать;
, следовательно, с повышением температуры тепловой эффект реакции будет возрастать; , следовательно, с повышением температуры тепловой эффект реакции уменьшается;
, следовательно, с повышением температуры тепловой эффект реакции уменьшается; .
. . (1.15)
. (1.15)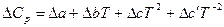 ,
, ,
,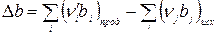 ,
,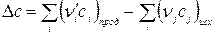 ,
, .
. .
. .
. для реагентов или принять, что
для реагентов или принять, что  не зависит от температуры в данном интервале.
не зависит от температуры в данном интервале. , (1.16)
, (1.16) .
. .
.


