
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 4.3. Использование свойств и графиков функций при решении уравнений и неравенств.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Графическое решение уравнений с одной переменной. На практике довольно часто оказывается, что решение уравнения Однако во многих случаях указанный выше метод графического решения уравнения не очень удобен. Так, для нахождения корней уравнения Так, для решения уравнения Ясно, что уравнение В первом случае надо строить графики функций Пример 1. Решить графически уравнение Заданное уравнение целесообразно переписать в виде
уравнение имеет два корня: -1; 2. Пример 2. Решить графически уравнение Построим в одной системе координат графики функций
Метод интервалов. Множество решений уравнений и неравенств с двумя переменными и их систем. Графическое решение систем уравнений Решить графически систему уравнений - это значит найти координаты общих точек графиков уравнений, построенных в одной системе координат. Графическое решение системы неравенств Решить графически систему неравенств – это значит найти область решений, координаты которой будут удовлетворять всем неравенствам системы. Примеры выполнения заданий.
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1540; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 сопряжено с громоздкими выкладками. В таких случаях прибегают к тому или иному методу приближенного решения уравнения. Мы рассмотрим графический метод, который, хотя и не обеспечивает хорошей точности, но является одним из наиболее простых. Он заключается в следующем: строят график функции
сопряжено с громоздкими выкладками. В таких случаях прибегают к тому или иному методу приближенного решения уравнения. Мы рассмотрим графический метод, который, хотя и не обеспечивает хорошей точности, но является одним из наиболее простых. Он заключается в следующем: строят график функции  и находят абсциссы точек пересечения графика с осью
и находят абсциссы точек пересечения графика с осью  . Так, для решения уравнения
. Так, для решения уравнения  достаточно построить график функции
достаточно построить график функции  и найти абсциссы точек пересечения этого графика с осыо
и найти абсциссы точек пересечения этого графика с осыо  потребовалось бы построить график функции
потребовалось бы построить график функции  , а это достаточно трудная задача. В подобных случаях уравнение
, а это достаточно трудная задача. В подобных случаях уравнение  , затем строят графики функций
, затем строят графики функций 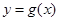 и
и  (если, разумеется, это проще, чем построение графика функции
(если, разумеется, это проще, чем построение графика функции  , затем построить графики функций
, затем построить графики функций  и
и  и найти абсциссы точек пересечения этих графиков.
и найти абсциссы точек пересечения этих графиков. ,
,  ,
,  .
. и
и  , во втором
, во втором  и
и  , в третьем
, в третьем  и
и  .
. .
. . Теперь решение уравнения может быть сведено к нахождению абсцисс точек пересечения графиков функций
. Теперь решение уравнения может быть сведено к нахождению абсцисс точек пересечения графиков функций  . На рис. 1 в одной системе координат построены графики функций
. На рис. 1 в одной системе координат построены графики функций  ;
;  . Таким образом, заданное
. Таким образом, заданное 
 .
. и
и  (рис. 2). Они пересекаются в точке А, абсцисса которой приближенно равна 1,3. Значит, заданное уравнение имеет единственное решение
(рис. 2). Они пересекаются в точке А, абсцисса которой приближенно равна 1,3. Значит, заданное уравнение имеет единственное решение  .
.
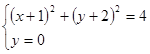
 - уравнение окружности с центром в точке (-1; -2) и радиусом r = 2
2. у = 0 – уравнение оси Ох
- уравнение окружности с центром в точке (-1; -2) и радиусом r = 2
2. у = 0 – уравнение оси Ох
 Общая точка: А(-1:0), значит х = -1, у = 0.
Проверка:
х=-1, у=0, то система примет вид:
Общая точка: А(-1:0), значит х = -1, у = 0.
Проверка:
х=-1, у=0, то система примет вид:  ,
,  ,
,  Значит, (-1;0) решение системы
Значит, (-1;0) решение системы

 у = х2 - квадратичная функция, график – парабола, ветви направлены вниз
у = 2х - линейная функция, график – прямая
1. А(0;-1), неравенство примет вид:
0-1<0(истинно), значит координаты всех точек внутренней области параболы без границы являются решениями первого неравенства.
2. В(-1;0), неравенство примет вид:
0+2>0(истинно), значит координаты всех точек области над прямой без границы являются решениями второго неравенства.
у = х2 - квадратичная функция, график – парабола, ветви направлены вниз
у = 2х - линейная функция, график – прямая
1. А(0;-1), неравенство примет вид:
0-1<0(истинно), значит координаты всех точек внутренней области параболы без границы являются решениями первого неравенства.
2. В(-1;0), неравенство примет вид:
0+2>0(истинно), значит координаты всех точек области над прямой без границы являются решениями второго неравенства.




