
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенства. Основные приемы их решения.Содержание книги Поиск на нашем сайте Линейные неравенства. Рассмотрим неравенства вида Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется частным решением неравенства. Решить неравенство с переменной — значит найти все его частные решения. Множество всех частных решений образует решение неравенства. Два неравенства с одной переменной х называются равносильными, если решения этих неравенств совпадают. Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному. Такие замены осуществляются на основе следующих утверждений. Если какой-либо член неравенства с переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному. Если обе части неравенства с переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному. Если обе части неравенства с переменной умножить или разделить на одно и то же отрицательное число, заменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному. Ниже на примерах мы покажем применение сформулированных утверждений для решения линейных неравенств, т.е. неравенств вида Пример 1. Решить неравенство Согласно утверждению 1, данное неравенство равносильно неравенству Разделам обе части неравенства Итак, неравенства Пример 2. Решить неравенство Раскрыв скобки, получим
Далее, имеем
Разделим теперь обе части неравенства на отрицательное число Пример 3. Решить неравенство
Освободимся от знаменателей, для чего умножим обе части на положительное число 6:
Далее, имеем
Таким образом, Пример 4. Решить неравенство
Последовательно получаем
Последнее неравенство верно при любом значении х, так как получается истинное высказывание 0 > —55. Поэтому решением данного неравенства является вся числовая прямая. Пример 5. Решить неравенство
Имеем:
Последнее неравенство не имеет решений, так как при любом значении переменной х получается ложное высказывание 0>2. Значит, и данное неравенство не имеет решений.
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

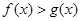 (соответственно
(соответственно 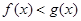 ,
,  ,
, 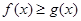 ), где
), где 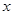 — переменная, а
— переменная, а 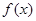 и
и 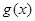 - выражения с переменной
- выражения с переменной 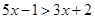 . При
. При 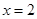 получаем
получаем 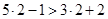 - истинное высказывание (верное числовое неравенство); при
- истинное высказывание (верное числовое неравенство); при 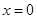 получаем
получаем 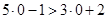 - ложное высказывание.
- ложное высказывание.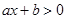 (соответственно
(соответственно  ,
, 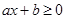 ,
, 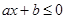 ), где
), где  и
и  - действительные числа, и для решения неравенств, сводимых к линейным.
- действительные числа, и для решения неравенств, сводимых к линейным.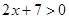 .
. (слагаемое 7 перенесено из одной части неравенства в другую с противоположным знаком, а знак данного неравенства оставлен без изменения).
(слагаемое 7 перенесено из одной части неравенства в другую с противоположным знаком, а знак данного неравенства оставлен без изменения). , равносильное неравенству
, равносильное неравенству 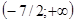 . Заметим, что решение данного неравенства можно записать в виде
. Заметим, что решение данного неравенства можно записать в виде 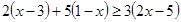 .
. ,
, .
. ,
,
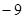 и изменим знак неравенства. Согласно утверждению 3, получим равносильное неравенство
и изменим знак неравенства. Согласно утверждению 3, получим равносильное неравенство 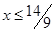 . Ответ можно также записать в виде
. Ответ можно также записать в виде  .
.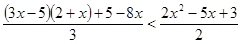 .
.
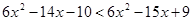 ,
,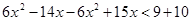 ,
,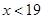 .
.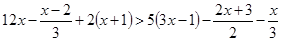 .
. ,
,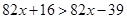 ,
,
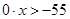
 .
. ,
, ,
,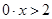 .
.


