
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения и системы уравнений.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Линейные уравнения. Уравнение вида Пример 1. Решить уравнение Данное уравнение — линейное; здесь I способ. Согласно теореме 1, уравнение II способ. Умножим обе части заданного уравнения на 15 (такое преобразование называется освобождением от знаменателей): Пример 2. Решить уравнение Освободимся от знаменателей, для чего умножим обе части уравнения на 21:
Далее, имеем:
Пример 3. Решить уравнение Последовательно получаем:
Перенесем все члены уравнения из правой части уравнения в левую, изменив при этом знаки:
После приведения подобный членов получаем
Уравнения с переменной в знаменателе. Рассмотрим уравнения вида Решение уравнения Таким образом, чтобы решить уравнение Пример 1. Решить уравнение Воспользовавшись указанным выше условием равенства дроби нулю, получим систему
Из уравнения Пример 2. Решить уравнение Имеем Из уравнения
Пример 3. Решить уравнение Имеем
Из уравнения Основные приемы их решения. Уравнение вида Числа a, b, c носят следующие названия a - первый коэффициент, b - второй коэффициент, c - свободный член. Выражение D = b2- 4ac называют дискриминантом квадратного уравнения.
Система вида Решением системы нелинейных уравнений является пара чисел (a, b), при подстановке которой в исходную систему получаются верные тождества: Нелинейные системы не имеют универсального способа решения, поэтому при решении конкретной системы уравнений нужно учитывать особенности заданных уравнений, переходя к равносильным системам. Основные методы решения систем нелинейных уравнений: · метод подстановки; · метод введения новых переменных; · графический метод; · метод алгебраического сложения; · метод почленного умножения и деления; · метод математического подбора. Системы нелинейных уравнений: примеры и достаточные знания, необходимые для решения заданий.
Метод подстановки. Метод подстановки: одно из уравнений системы преобразуют к виду, разрешенному относительно одной переменной, например у выражают через х. Далее, полученное выражение подставляют вместо у во второе уравнение. В результате получается уравнение с одной переменной х. Находят корни этого уравнения, а затем, воспользовавшись выражением у через х, находят соответствующие значения у. Пример 1. Решить систему уравнений
Из первого уравнения находим
и, далее,
Соответствующие значения х найдем из уравнения Пример 2. Решить систему уравнений
Из второго уравнения системы находим
28 = 1. Полученное высказывание является ложным при любом х. Это значит, что заданная система уравнений не имеет решений.
Метод сложения. Суть этого метода поясним на примерах. Пример 1. Решить систему уравнений
Умножив обе части второго уравнения системы на 3, получим систему
равносильную данной на основании теоремы 1. Сложим теперь оба уравнения полученной системы. Согласно теореме 2, система
равносильна системе (**). Система (***) преобразуется к виду
Из уравнения Итак, (5; - 1) —решение системы (***), а значит, и решение равносильной ей системы (*). Тема 4.2. Неравенства.
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 647; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.156.153 (0.011 с.) |

 , где
, где 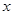 — переменная, а
— переменная, а  и
и  — действительные числа, причем
— действительные числа, причем 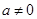 , называется линейным уравнением. Числа
, называется линейным уравнением. Числа  .
. ,
,  . Решение проведем двумя способами.
. Решение проведем двумя способами. равносильно данному. Разделим обе части этого уравнения на коэффициент при
равносильно данному. Разделим обе части этого уравнения на коэффициент при  — корень уравнения.
— корень уравнения. . В силу теоремы 2, полученное уравнение равносильно данному. Далее, имеем:
. В силу теоремы 2, полученное уравнение равносильно данному. Далее, имеем:  ,
,  .
. .
. ;
; ;
; ;
;
 .
. .
. ;
; .
. .
.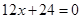 ,
, ,
,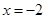 .
. , где
, где  — многочлен, а также уравнения, сводимые к указанному виду. Эти уравнения не являются линейными, но в процессе решения они сводятся к линейным.
— многочлен, а также уравнения, сводимые к указанному виду. Эти уравнения не являются линейными, но в процессе решения они сводятся к линейным. равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен, от нуля (на нуль делить нельзя!). Это записывают так:
равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен, от нуля (на нуль делить нельзя!). Это записывают так: 
 . Если это высказывание истинно, то найденный корень линейного уравнения
. Если это высказывание истинно, то найденный корень линейного уравнения  ), то уравнение
), то уравнение  .
.
 находим
находим  . Так как высказывание
. Так как высказывание  истинно, то
истинно, то  .
.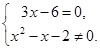 .
. находим
находим  . Высказывание
. Высказывание  ложно; значит, данное уравнение не имеет корней.
ложно; значит, данное уравнение не имеет корней. .
. ,
, ,
, ,
, .
. находим
находим  . Высказывание
. Высказывание  истинно; значит,
истинно; значит,  , где a, b, c - действительные числа, причем a≠0, называют квадратным уравнением.
, где a, b, c - действительные числа, причем a≠0, называют квадратным уравнением.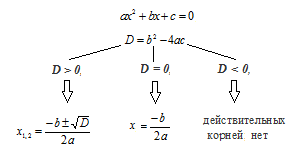
 , называется системой нелинейных уравнений с двумя переменными, если хотя бы одно из уравнений нелинейное.
, называется системой нелинейных уравнений с двумя переменными, если хотя бы одно из уравнений нелинейное. .
.
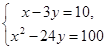
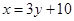 . Подставим выражение
. Подставим выражение 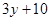 вместо х во второе уравнение системы; тогда
вместо х во второе уравнение системы; тогда
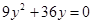 ,
, 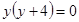 ,
, 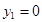 ,
, 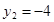 .
.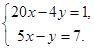
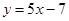 . Подставив выражение
. Подставив выражение 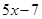 вместо у в первое уравнение системы, имеем
вместо у в первое уравнение системы, имеем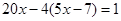 ,
,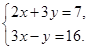 (*)
(*) (**)
(**)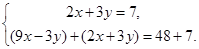 (***)
(***)
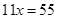 находим х=5. Подставив это значение в уравнение 2х+3у=7, получим у = -1.
находим х=5. Подставив это значение в уравнение 2х+3у=7, получим у = -1.


