
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1.1. Развитие понятия о числе.Содержание книги Поиск на нашем сайте
Конспект лекций
по дисциплине: ОД.03. Математика: алгебра и начала математического анализа, геометрия
(1 курс 1 семестр)
Содержание: Раздел 1. Алгебра. 3 Тема 1.1. Развитие понятия о числе. 3 Действительные числа. 3 Комплексные числа. 4 Нахождение приближенных значений величин и погрешностей вычислений. 5 Тема 1.2. Корни, степени. 9 Степени с действительными показателями. 9 Решение иррациональных уравнений. 10 Решение показательных уравнений. 11 Тема 1.3. Логарифм. 11 Логарифм числа. 11 Виды логарифмов. 11 Действия с логарифмами. 12 Нахождение значений логарифма. 12 Переход к новому основанию. 12 Решение логарифмических уравнений. 13 Логарифмирование и потенцирование выражений. 13 Раздел 2. Основы тригонометрии. 14 Тема 2.1. Основные понятия. 14 Радианная мера угла. 14 Синус, косинус, тангенс и котангенс числа. 14 Тема 2.2. Основные тригонометрические тождества. 15 Основные тригонометрические тождества. 15 Формулы приведения. 17 Формулы сложения. 17 Формулы удвоения. 18 Формулы половинного угла. 18 Тема 2.3. Преобразования простейших тригонометрических выражений. 18 Формула суммы тригонометрических функций. Т ангенс половинного аргумента. 18 Тема 2.4. Арксинус, арккосинус, арктангенс числа. 20 Обратные тригонометрические функции. 20 Тема 2.5. Тригонометрические уравнения и неравенства. 20 Простейшие тригонометрические уравнения. 20 Решение тригонометрических уравнений. 21 Простейшие тригонометрические неравенства. 21 Раздел 3. Функции и графики. 23 Тема 3.1. Функции. Свойства функций. 23 Функции. Построение графиков функций. Свойства функции. 23 Сложная функция (композиция). 26 Обратные функции. График обратной функции. 26 Тема 3.2. Степенные, показательные, логарифмические и тригонометрические функции. Обратные тригонометрические функции. 28 Степенная функция, свойства и график. 28 Линейная, квадратичная, кусочно-линейная и дробно-линейная функции. 28 Показательная и логарифмическая функции, их свойства и графики. 28 Определения тригонометрических функций, их свойства и графики. 30
Обратные тригонометрические функции. 30 Преобразования графиков функций. 31 Раздел 4. Уравнения и неравенства. 33 Тема 4.1. Уравнения и системы уравнений. 33 Уравнения и системы уравнений. 33 Основные приемы их решения. 34 Тема 4.2. Неравенства. 36 Неравенства. Основные приемы их решения. 36 Тема 4.3. Использование свойств и графиков функций при решении уравнений и неравенств. 42 Метод интервалов. 43 Множество решений уравнений и неравенств с двумя переменными и их систем. 43
Раздел 1. Алгебра. Тема 1.1. Развитие понятия о числе. Действительные числа. Множество вещественных чисел состоит из рациональных и иррациональных чисел. Рациональным называется число, которое можно представить в виде Обозначение некоторых числовых множеств:
Перечислим основные свойства вещественных чисел. I. Сложение и умножение вещественных чисел. Для любой пары 10. 20. 30. 40. 50. 60.Существует единственное число 0 такое, что
70. Для любого числа 80. Существует единственное число 90. Для любого числа II. Сравнение вещественных чисел. Для любых двух вещественных чисел Отношение > обладает следующими свойствами. Каковы бы ни были числа 100. Если 110. Если 120. Если Вместо III. Непрерывность вещественных чисел. 130. Пусть X и Y – два множества, состоящие из вещественных чисел. Тогда, если для любых чисел (Свойством непрерывности не обладает множество только рациональных чисел.)
Из свойств I, II и III вытекают все остальные свойства вещественных чисел: 140. Число
150. Число Число 160. Если 170. Если 180. Если 190. 200. 210. 220. 230. Если 240. Если 250. Если 260. Если
Свойства I-III называются аксиомами вещественных чисел. Комплексные числа.
Тема 1.2. Корни, степени Примеры выполнения заданий. Пример 1. Вычислить: Решение: Ответ: 8. Пример 2. Вычислить: Решение: Ответ: 15. Пример 3. Вычислить: Решение: Ответ: 5. Пример 4. Упростить: Решение: Ответ: а-2в13. Пример 5. Тема 1.3. Логарифм. Логарифм числа. Логарифмом числа Из определения следует, что нахождение Виды логарифмов. Наиболее широкое применение нашли следующие виды логарифмов. · Натуральные логарифмы: · Десятичные логарифмы: Действия с логарифмами. Основное логарифмическое тождество Из равенства двух логарифмов следует равенство логарифмируемых выражений. В самом деле, если Логарифмы единицы и числа, равного основанию логарифма Логарифм произведения, частного от деления, степени и корня:
Переход к новому основанию.
Примеры выполнения заданий.
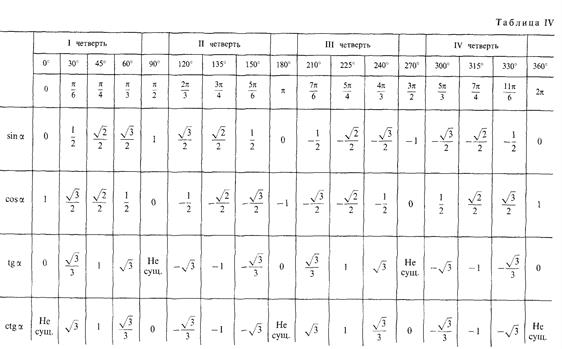
Тема 2.1. Основные понятия. Радианная мера угла.
Примеры выполнения заданий.
Формулы приведения.
Формулы сложения.
Формулы удвоения
Формулы половинного угла.
Тема 2.3. Преобразования простейших тригонометрических выражений. Формула суммы тригонометрических функций. Т ангенс половинного аргумента. Формулы преобразования суммы и разности тригонометрических функций в произведение
Формулы преобразования произведения тригонометрических функций в сумму
Примеры выполнения заданий. Пример 1. Преобразовать в произведение: Решение: В необходимую формулу подставим данные значения:
Ответ: Пример 2. Преобразовать в сумму: Решение: В необходимую формулу подставим данные значения:
Ответ: Пример 3. Доказать тождество: Решение: Разложим произведение
Подставим полученное выражение, получим
Так как Ответ: что и требовалось доказать. Примеры выполнения заданий.
Определения тригонометрических функций, их свойства и графики.
Основные приемы их решения. Уравнение вида Числа a, b, c носят следующие названия a - первый коэффициент, b - второй коэффициент, c - свободный член. Выражение D = b2- 4ac называют дискриминантом квадратного уравнения.
Система вида Решением системы нелинейных уравнений является пара чисел (a, b), при подстановке которой в исходную систему получаются верные тождества: Нелинейные системы не имеют универсального способа решения, поэтому при решении конкретной системы уравнений нужно учитывать особенности заданных уравнений, переходя к равносильным системам. Основные методы решения систем нелинейных уравнений: · метод подстановки; · метод введения новых переменных; · графический метод; · метод алгебраического сложения; · метод почленного умножения и деления; · метод математического подбора. Системы нелинейных уравнений: примеры и достаточные знания, необходимые для решения заданий.
Метод подстановки. Метод подстановки: одно из уравнений системы преобразуют к виду, разрешенному относительно одной переменной, например у выражают через х. Далее, полученное выражение подставляют вместо у во второе уравнение. В результате получается уравнение с одной переменной х. Находят корни этого уравнения, а затем, воспользовавшись выражением у через х, находят соответствующие значения у. Пример 1. Решить систему уравнений
Из первого уравнения находим
и, далее,
Соответствующие значения х найдем из уравнения Пример 2. Решить систему уравнений
Из второго уравнения системы находим
28 = 1. Полученное высказывание является ложным при любом х. Это значит, что заданная система уравнений не имеет решений. Метод сложения. Суть этого метода поясним на примерах. Пример 1. Решить систему уравнений
Умножив обе части второго уравнения системы на 3, получим систему
равносильную данной на основании теоремы 1. Сложим теперь оба уравнения полученной системы. Согласно теореме 2, система
равносильна системе (**). Система (***) преобразуется к виду
Из уравнения Итак, (5; - 1) —решение системы (***), а значит, и решение равносильной ей системы (*). Тема 4.2. Неравенства. Линейные неравенства. Рассмотрим неравенства вида Всякое значение переменной, при котором данное неравенство с переменной обращается в верное числовое неравенство, называется частным решением неравенства. Решить неравенство с переменной — значит найти все его частные решения. Множество всех частных решений образует решение неравенства. Два неравенства с одной переменной х называются равносильными, если решения этих неравенств совпадают. Основная идея решения неравенства состоит в следующем: мы заменяем данное неравенство другим, более простым, но равносильным данному. Такие замены осуществляются на основе следующих утверждений. Если какой-либо член неравенства с переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному. Если обе части неравенства с переменной умножить или разделить на одно и то же отрицательное число, заменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному. Ниже на примерах мы покажем применение сформулированных утверждений для решения линейных неравенств, т.е. неравенств вида
Пример 1. Решить неравенство Согласно утверждению 1, данное неравенство равносильно неравенству Разделам обе части неравенства Итак, неравенства Пример 2. Решить неравенство Раскрыв скобки, получим
Далее, имеем
Разделим теперь обе части неравенства на отрицательное число Пример 3. Решить неравенство
Освободимся от знаменателей, для чего умножим обе части на положительное число 6:
Далее, имеем
Таким образом, Пример 4. Решить неравенство
Последовательно получаем
Последнее неравенство верно при любом значении х, так как получается истинное высказывание 0 > —55. Поэтому решением данного неравенства является вся числовая прямая. Пример 5. Решить неравенство
Имеем:
Последнее неравенство не имеет решений, так как при любом значении переменной х получается ложное высказывание 0>2. Значит, и данное неравенство не имеет решений. Квадратные неравенства. Рассмотрим функцию
На основании графической иллюстрации можно сделать следующие выводы о решении квадратного неравенства: 1) есди 2) если 3) если Запоминать этот вывод не следует; его всегда можно получить с помощью приведенной выше графической иллюстрации. Пример 1. Решить неравенство: а) б) в) г) а) Из уравнения б) Прежде всего, умножив обе части неравенства на в) Здесь г) Прежде всего, умножив обе части неравенства на Пример 2. Найти область определения функции
Задача сводится к решению неравенства Пример 3. Решить неравенство Имеем
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 5513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.88.176 (0.015 с.) |

 , где
, где 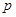 и
и 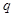 - целые числа, причем
- целые числа, причем 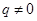 . Иррациональным называется всякое вещественное число, которое не является рациональным. Всякое рациональное число является либо целым, либо представляется конечной или периодической бесконечной десятичной дробью. Иррациональное же число представляется непериодической бесконечной десятичной дробью. Например, рациональные числа
. Иррациональным называется всякое вещественное число, которое не является рациональным. Всякое рациональное число является либо целым, либо представляется конечной или периодической бесконечной десятичной дробью. Иррациональное же число представляется непериодической бесконечной десятичной дробью. Например, рациональные числа  и
и 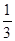 можно представить в виде следующих десятичных дробей:
можно представить в виде следующих десятичных дробей:  ;
; 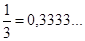 ; иррациональные числа
; иррациональные числа 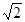 и
и  - в виде непериодических бесконечных десятичных дробей:
- в виде непериодических бесконечных десятичных дробей: 
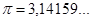
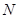 - множество натуральных чисел – числа, используемые при счете,
- множество натуральных чисел – числа, используемые при счете,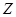 - множество целых чисел – это натуральные числа, числа, противоположные натуральным и число 0,
- множество целых чисел – это натуральные числа, числа, противоположные натуральным и число 0,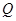 - множество рациональных чисел – целые числа и дроби (положительные и отрицательные),
- множество рациональных чисел – целые числа и дроби (положительные и отрицательные),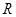 - множество действительных чисел – рациональные и иррациональные числа.
- множество действительных чисел – рациональные и иррациональные числа.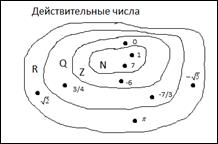

 и
и 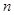 вещественных чисел определены и при том единственным образом два вещественных числа
вещественных чисел определены и при том единственным образом два вещественных числа 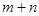 и
и  , называемых соответственно их суммой и произведением, причем имеют место следующие свойства. Каковы бы ни были числа
, называемых соответственно их суммой и произведением, причем имеют место следующие свойства. Каковы бы ни были числа  :
: - переместительный закон сложения.
- переместительный закон сложения. - сочетательный закон сложения.
- сочетательный закон сложения.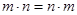 - переместительный закон умножения.
- переместительный закон умножения. - сочетательный закон умножения.
- сочетательный закон умножения.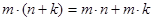 - распределительный закон умножения относительно сложения.
- распределительный закон умножения относительно сложения.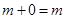 для любого числа
для любого числа 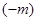 , что
, что 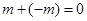 .
.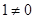 такое, что для любого числа
такое, что для любого числа 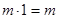 .
.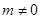 существует такое число
существует такое число 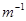 , что
, что 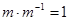 ; число
; число 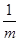 .
.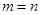 (
(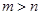 (
(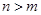 . Отношение = обладает свойством: если
. Отношение = обладает свойством: если 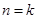 , то
, то  .
. , то
, то 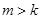 .
.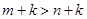 .
. и
и 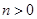 , то
, то 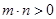 .
. (
(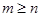 или, что то же,
или, что то же,  ) означает, что либо
) означает, что либо  ,
,  называют неравенствами. Неравенства
называют неравенствами. Неравенства 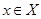 и
и  выполняется неравенство
выполняется неравенство 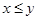 , то существует хотя бы одно число
, то существует хотя бы одно число 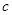 такое, что для всех таких
такое, что для всех таких 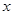 и
и 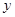 выполняется неравенство
выполняется неравенство  .
.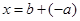 является решением уравнения
является решением уравнения 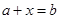 .
.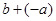 - разность чисел
- разность чисел  и
и  , обозначается
, обозначается  .
.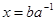 является решением уравнения
является решением уравнения 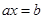 , если
, если 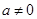 .
. называется частным чисел
называется частным чисел 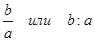 .
.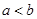 , то
, то 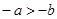 .
.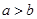 и
и 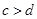 , то
, то 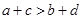 .
.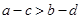 .
. .
.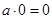 .
.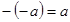 .
. .
. и
и 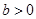 , то
, то 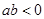 .
.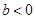 , то
, то 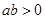 .
.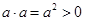 .
.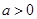 , то
, то 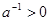 .
.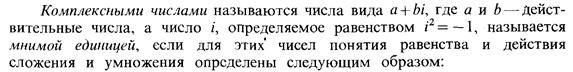

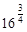 .
.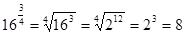
 .
.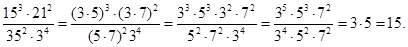
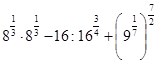

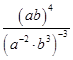 .
.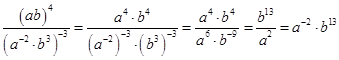
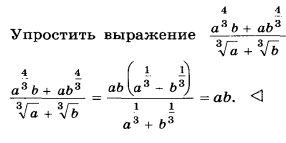
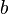 по основанию
по основанию 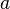 называется показатель степени, в которую надо возвести основание
называется показатель степени, в которую надо возвести основание 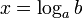 равносильно решению уравнения
равносильно решению уравнения 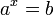 . Например,
. Например,  потому что
потому что 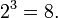
 , основание: число Эйлера (е)
, основание: число Эйлера (е) , основание: число 10
, основание: число 10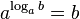
 , то
, то  , откуда, согласно основному тождеству:
, откуда, согласно основному тождеству: 



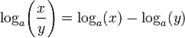


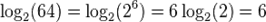
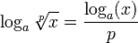
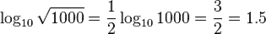


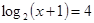

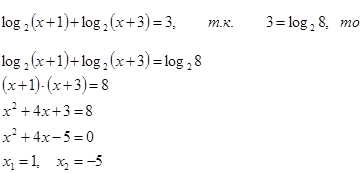 Проверка
Проверка
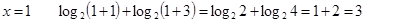 - левая часть
3=3
- левая часть
3=3 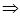 х = 1 – корень уравнения
х = 1 – корень уравнения
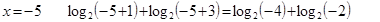 - левая часть не имеет смысла
- левая часть не имеет смысла 
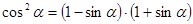
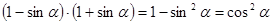 - правая часть
- правая часть 
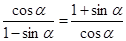
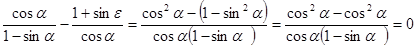




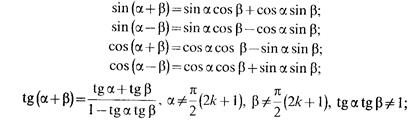
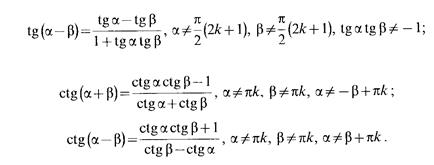
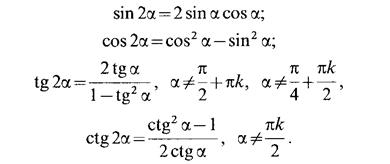
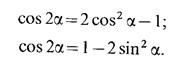

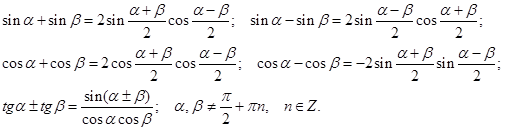
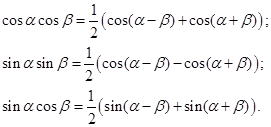
 .
.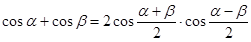

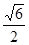


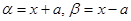

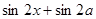
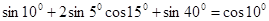
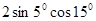 на сумму по формуле, получим:
на сумму по формуле, получим: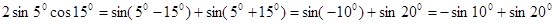
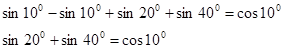
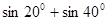 - преобразуем по формуле
- преобразуем по формуле 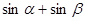 , получим
, получим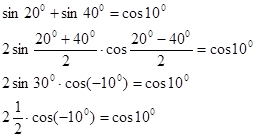
 , то
, то 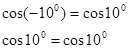
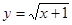
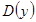 : х ≥ -1
: х ≥ -1
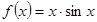
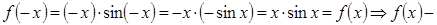 чётная
чётная
 периодическая с периодом
периодическая с периодом 
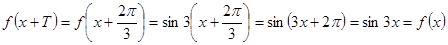





 , где a, b, c - действительные числа, причем a≠0, называют квадратным уравнением.
, где a, b, c - действительные числа, причем a≠0, называют квадратным уравнением.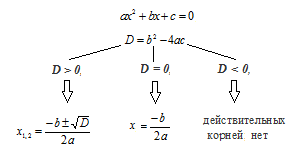
 , называется системой нелинейных уравнений с двумя переменными, если хотя бы одно из уравнений нелинейное.
, называется системой нелинейных уравнений с двумя переменными, если хотя бы одно из уравнений нелинейное. .
.
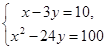
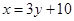 . Подставим выражение
. Подставим выражение 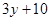 вместо х во второе уравнение системы; тогда
вместо х во второе уравнение системы; тогда
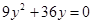 ,
, 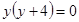 ,
, 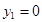 ,
, 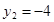 .
.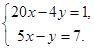
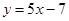 . Подставив выражение
. Подставив выражение 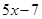 вместо у в первое уравнение системы, имеем
вместо у в первое уравнение системы, имеем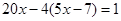 ,
,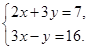 (*)
(*) (**)
(**)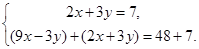 (***)
(***)
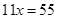 находим х=5. Подставив это значение в уравнение 2х+3у=7, получим у = -1.
находим х=5. Подставив это значение в уравнение 2х+3у=7, получим у = -1.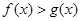 (соответственно
(соответственно 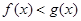 ,
,  ,
, 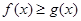 ), где
), где 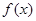 и
и 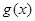 - выражения с переменной
- выражения с переменной 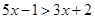 . При
. При 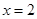 получаем
получаем 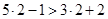 - истинное высказывание (верное числовое неравенство); при
- истинное высказывание (верное числовое неравенство); при 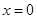 получаем
получаем 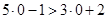 - ложное высказывание.
- ложное высказывание.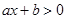 (соответственно
(соответственно  ,
, 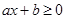 ,
, 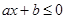 ), где
), где 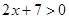 .
. (слагаемое 7 перенесено из одной части неравенства в другую с противоположным знаком, а знак данного неравенства оставлен без изменения).
(слагаемое 7 перенесено из одной части неравенства в другую с противоположным знаком, а знак данного неравенства оставлен без изменения). , равносильное неравенству
, равносильное неравенству 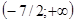 . Заметим, что решение данного неравенства можно записать в виде
. Заметим, что решение данного неравенства можно записать в виде 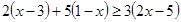 .
. ,
, .
. ,
,
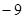 и изменим знак неравенства. Согласно утверждению 3, получим равносильное неравенство
и изменим знак неравенства. Согласно утверждению 3, получим равносильное неравенство 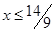 . Ответ можно также записать в виде
. Ответ можно также записать в виде  .
.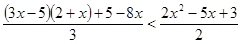 .
.
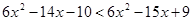 ,
,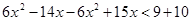 ,
,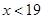 .
.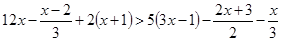 .
. ,
,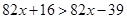 ,
,
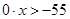
 .
. ,
, ,
,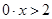 .
.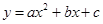 , где
, где 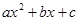 положителен; 2) иметь с осью Ох только одну общую точку (рис. 6, б) — в случае D = 0; 3) лежать выше оси Ох (рис. 6, в) — в случае D < О.
положителен; 2) иметь с осью Ох только одну общую точку (рис. 6, б) — в случае D = 0; 3) лежать выше оси Ох (рис. 6, в) — в случае D < О.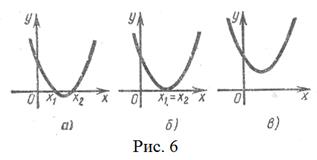
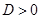 , то решением неравенства
, то решением неравенства  служит объединение двух открытых лучей:
служит объединение двух открытых лучей: 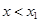 ;
; 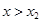 , а решением неравенства
, а решением неравенства 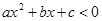 служит интервал
служит интервал 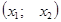 , здесь х1, х2 — корни трехчлена, причем х1 <х2;
, здесь х1, х2 — корни трехчлена, причем х1 <х2;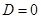 , то неравенство
, то неравенство  , а неравенство
, а неравенство  справедливо при всех х; неравенство
справедливо при всех х; неравенство 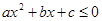 выполняется лишь в точке
выполняется лишь в точке 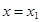 ;
; , то неравенства
, то неравенства 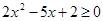 ;
; ;
;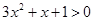 ;
;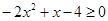 .
.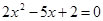 находим
находим 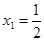 ;
; 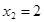 . Неравенству удовлетворяют все значения х, лежащие вне промежутка между корнями:
. Неравенству удовлетворяют все значения х, лежащие вне промежутка между корнями:  или
или 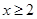 .
.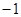 , получим
, получим  и, далее, (х+2)2>0. Этому неравенству удовлетворяют любые значения х, кроме
и, далее, (х+2)2>0. Этому неравенству удовлетворяют любые значения х, кроме 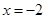 .
. . Значит, неравенство
. Значит, неравенство 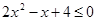 . Здесь
. Здесь 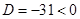 ; значит, неравенство
; значит, неравенство 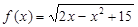 .
.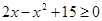 , поскольку выражение, стоящее под знаком квадратного корня, должно быть неотрицательным. Далее, имеем
, поскольку выражение, стоящее под знаком квадратного корня, должно быть неотрицательным. Далее, имеем  . Корни трехчлена
. Корни трехчлена 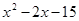 таковы:
таковы: 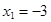 ;
; 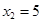 . Решением неравенства служит отрезок
. Решением неравенства служит отрезок  .
.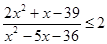 .
.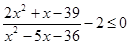 ,
,


