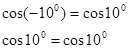Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение логарифмических уравнений.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения, содержащие неизвестное под знаком логарифма, называются логарифмическими. Такие уравнения решаются: а) с помощью определения логарифма, б) с помощью теорем о логарифмах, с) с помощью утверждений о том, что если положительные числа равны, то и равны их логарифмы при данном основании и обратно, если логарифмы чисел равны, то равны и соответствующие им числа. Во всех случаях полученные решения необходимо проверить подстановкой их в данное уравнение и исключить посторонний корень. Часто используется формула перехода от одного основания к другому Примеры выполнения заданий.
Логарифмирование и потенцирование выражений.
Раздел 2. Основы тригонометрии. Тема 2.1. Основные понятия. Радианная мера угла.
Синус, косинус, тангенс и котангенс числа.
Определение тригонометрических функций:
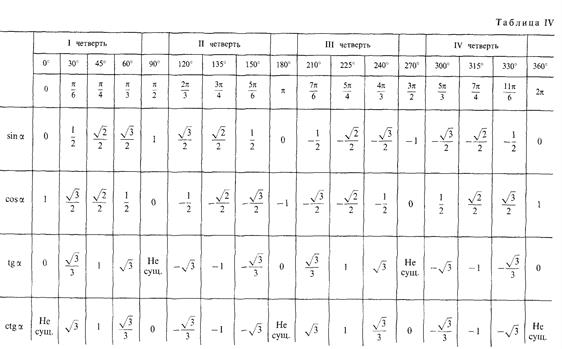
Определение: синусом угла поворота называется ордината точки, изображающей данный угол. Определение: косинусом угла поворота называется абсцисса точки, изображающей данный угол. Определение: тангенсом угла поворота называется отношение ординаты точки, изображающей угол, к ее абсциссе. Определение: котангенсом угла поворота называется отношение абсциссы точки, изображающей данный угол к ее ординате. Значения тригонометрических функций некоторых углов
Тема 2.2. Основные тригонометрические тождества. Основные тригонометрические тождества.
При доказательстве тригонометрических тождеств обычно используют следующие способы: 1. Выражение, стоящее в одной части равенства, с помощью тождественных преобразований приводят к выражению, стоящему в другой части равенства. 2. Выражения, стоящие в левой и правой части тождества с помощью тождественных преобразований приводят к одному и тому же виду. 3. Доказывают, что разность между левой и правой частью тождества равны нулю. При доказательстве тригонометрических тождеств используют: 1. основные соотношения между тригонометрическими функциями одного и того же аргумента, 2. формулы приведения, формулы сложения, 3. формулы для двойного и половинного аргумента, 4. формулы преобразования суммы тригонометрических функций в произведение, 5. числовые значения тригонометрических функций для некоторых углов. Примеры выполнения заданий.
Формулы приведения.
Формулы сложения.
Формулы удвоения
Формулы половинного угла.
Тема 2.3. Преобразования простейших тригонометрических выражений. Формула суммы тригонометрических функций. Т ангенс половинного аргумента. Формулы преобразования суммы и разности тригонометрических функций в произведение
Формулы преобразования произведения тригонометрических функций в сумму
Примеры выполнения заданий. Пример 1. Преобразовать в произведение: Решение: В необходимую формулу подставим данные значения:
Ответ: Пример 2. Преобразовать в сумму: Решение: В необходимую формулу подставим данные значения:
Ответ: Пример 3. Доказать тождество: Решение: Разложим произведение
Подставим полученное выражение, получим
Так как Ответ: что и требовалось доказать.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 977; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.008 с.) |


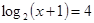

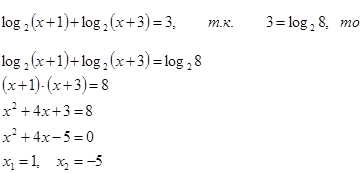 Проверка
Проверка
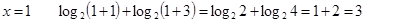 - левая часть
3=3
- левая часть
3=3 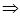 х = 1 – корень уравнения
х = 1 – корень уравнения
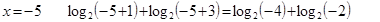 - левая часть не имеет смысла
- левая часть не имеет смысла 




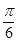

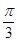






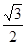



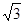


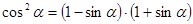
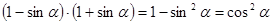 - правая часть
- правая часть 
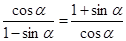
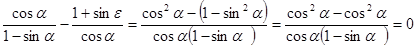




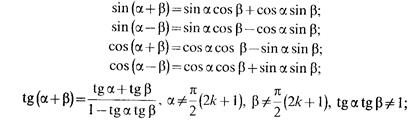
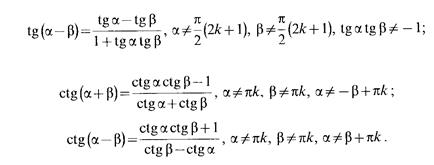
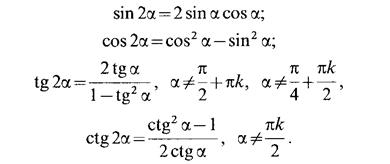
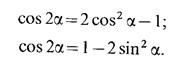

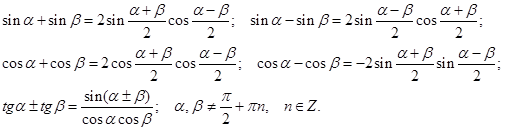
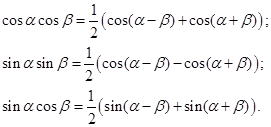
 .
.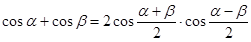

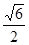


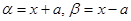

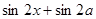
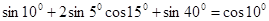
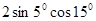 на сумму по формуле, получим:
на сумму по формуле, получим: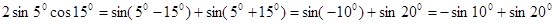
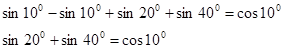
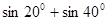 - преобразуем по формуле
- преобразуем по формуле 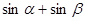 , получим
, получим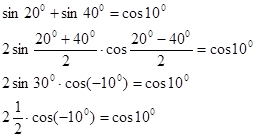
 , то
, то