
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системы и совокупности неравенств.Содержание книги Поиск на нашем сайте
Несколько неравенств с одной переменной образуют систему, если ставится задача найти все общие решения заданных неравенств. Значение переменной, при котором каждое из неравенств обращается в верное числовое неравенство, называется решением системы неравенств. Неравенства, образующие систему, объединяются фигурной скобкой. Например, запись Иногда используется запись в виде двойного неравенства. Например, систему неравенств Несколько неравенств с одной переменной образуют совокупность, если ставится задача найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Значение переменной, при котором хотя бы одно из неравенств, образующих совокупность, обращается в верное числовое неравенство, называется решением совокупности неравенств. Неравенства, образующие совокупность, записываются в строчку и отделяются друг от друга знаком «;». Например, запись 2х—5<1; Зх+2>7 означает, что неравенства образуют совокупность. Иногда для обозначения совокупности неравенств используется квадратная скобка. Так, запись Рассмотрим примеры решения систем и совокупностей неравенств. В этом параграфе ограничимся линейными неравенствами и неравенствами, сводящимися к линейным. Пример 1. Решить систему неравенств
Первое неравенство системы преобразуется в равносильное ему неравенство
Пример 2. Решить систему неравенств
Выполнив преобразования каждого из неравенств системы, получим систему
Пример 3. Решить систему неравенств
После преобразований получим систему Решением первого неравенства этой системы служит вся числовая прямая, а второго неравенства — промежуток Пример 4. Решить систему неравенств После преобразований получим систему Так как первое неравенство системы не имеет решений, то и система не имеет решений. Пример 5. Решить совокупность неравенств
Преобразовав каждое из неравенств, получим совокупность
Пример 6. Решить неравенство Значение дроби положительно тогда и только тогда, когда числитель и знаменатель имеют значения одного знака, т. е. когда
Можно сказать, что заданное неравенство равносильно совокупности двух систем
Решение первой системы — промежуток Пример 7. Решить неравенство Преобразуем заданное неравенство:
Разделим обе части последнего неравенства на —5:
Решение первой системы — промежуток Квадратные неравенства. Рассмотрим функцию
На основании графической иллюстрации можно сделать следующие выводы о решении квадратного неравенства: 1) есди 2) если 3) если Запоминать этот вывод не следует; его всегда можно получить с помощью приведенной выше графической иллюстрации. Пример 1. Решить неравенство: а) б)
в) г) а) Из уравнения б) Прежде всего, умножив обе части неравенства на в) Здесь г) Прежде всего, умножив обе части неравенства на Пример 2. Найти область определения функции
Задача сводится к решению неравенства Пример 3. Решить неравенство Имеем
Теперь задача сводится к решению совокупности двух систем:
Решим первую систему. Из неравенства Решим вторую систему. Из неравенства
Итак, заданному неравенству удовлетворяют все такие числа х, что
|
||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 1528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.221.115 (0.009 с.) |

 означает, что неравенства
означает, что неравенства  и
и  образуют систему.
образуют систему. можно записать в виде двойного неравенства
можно записать в виде двойного неравенства  .
. означает, что неравенства образуют совокупность.
означает, что неравенства образуют совокупность.
 , второе — в неравенство
, второе — в неравенство  . Таким образом, приходим к системе
. Таким образом, приходим к системе  . Решением служит интервал
. Решением служит интервал  (рис. 1).
(рис. 1).

 , которая не имеет решений (рис. 2).
, которая не имеет решений (рис. 2).

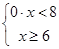 .
. . Этот промежуток и является решением системы.
. Этот промежуток и является решением системы. .
. .
.
 , решением которой служит луч
, решением которой служит луч  (рис.3).
(рис.3).
 .
.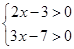 , или
, или  .
.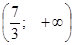 , решение второй системы — промежуток
, решение второй системы — промежуток  . Объединив эти множества, получим решение совокупности систем, а вместе с тем и заданного неравенства: х<3/2: х>7/3.
. Объединив эти множества, получим решение совокупности систем, а вместе с тем и заданного неравенства: х<3/2: х>7/3. .
. ;
; 
 . Значение дроби отрицательно в том и только в том случае, когда числитель и знаменатель имеют значения противоположных знаков; дробь обращается в нуль, когда числитель равен нулю, а знаменатель отличен от нуля. Воспользовавшись этим замечанием, приходим к следующей совокупности двух систем:
. Значение дроби отрицательно в том и только в том случае, когда числитель и знаменатель имеют значения противоположных знаков; дробь обращается в нуль, когда числитель равен нулю, а знаменатель отличен от нуля. Воспользовавшись этим замечанием, приходим к следующей совокупности двух систем: ;
;  .
. , вторая система не имеет решений. Значит, решение совокупности, а поэтому и заданного неравенства — промежуток
, вторая система не имеет решений. Значит, решение совокупности, а поэтому и заданного неравенства — промежуток 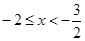 .
.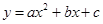 , где
, где 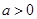 . Ее графиком, как известно, является парабола с ветвями, направленными вверх. Эта парабола может: 1) пересечь ось Ох в двух точках (рис. 6, а) — так обстоит дело в случае, если дискриминант D трехчлена
. Ее графиком, как известно, является парабола с ветвями, направленными вверх. Эта парабола может: 1) пересечь ось Ох в двух точках (рис. 6, а) — так обстоит дело в случае, если дискриминант D трехчлена 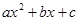 положителен; 2) иметь с осью Ох только одну общую точку (рис. 6, б) — в случае D = 0; 3) лежать выше оси Ох (рис. 6, в) — в случае D < О.
положителен; 2) иметь с осью Ох только одну общую точку (рис. 6, б) — в случае D = 0; 3) лежать выше оси Ох (рис. 6, в) — в случае D < О.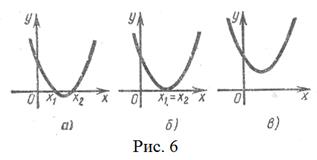
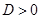 , то решением неравенства
, то решением неравенства  служит объединение двух открытых лучей:
служит объединение двух открытых лучей: 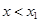 ;
; 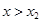 , а решением неравенства
, а решением неравенства 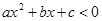 служит интервал
служит интервал 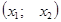 , здесь х1, х2 — корни трехчлена, причем х1 <х2;
, здесь х1, х2 — корни трехчлена, причем х1 <х2;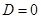 , то неравенство
, то неравенство  , а неравенство
, а неравенство  справедливо при всех х; неравенство
справедливо при всех х; неравенство 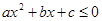 выполняется лишь в точке
выполняется лишь в точке 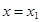 ;
; , то неравенства
, то неравенства 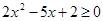 ;
; ;
;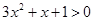 ;
;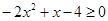 .
.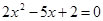 находим
находим 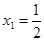 ;
; 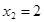 . Неравенству удовлетворяют все значения х, лежащие вне промежутка между корнями:
. Неравенству удовлетворяют все значения х, лежащие вне промежутка между корнями:  или
или 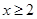 .
.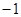 , получим
, получим  и, далее, (х+2)2>0. Этому неравенству удовлетворяют любые значения х, кроме
и, далее, (х+2)2>0. Этому неравенству удовлетворяют любые значения х, кроме 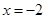 .
. . Значит, неравенство
. Значит, неравенство 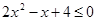 . Здесь
. Здесь 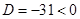 ; значит, неравенство
; значит, неравенство 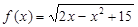 .
.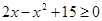 , поскольку выражение, стоящее под знаком квадратного корня, должно быть неотрицательным. Далее, имеем
, поскольку выражение, стоящее под знаком квадратного корня, должно быть неотрицательным. Далее, имеем  . Корни трехчлена
. Корни трехчлена 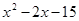 таковы:
таковы: 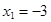 ;
; 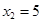 . Решением неравенства служит отрезок
. Решением неравенства служит отрезок  .
.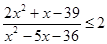 .
.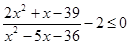 ,
,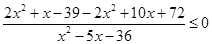 ,
,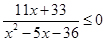 .
. или
или  .
. находим
находим  . Трехчлен
. Трехчлен 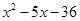 имеет корни
имеет корни  и
и 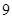 ; значит, решением неравенства
; значит, решением неравенства  служит интервал
служит интервал  . Решением системы является промежуток
. Решением системы является промежуток  (рис. 7).
(рис. 7).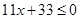 находим
находим  , из неравенства
, из неравенства  получаем
получаем  или
или  . Решением системы является промежуток
. Решением системы является промежуток  (рис. 8).
(рис. 8).
 ;
; 


