
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Построение аксонометрических изображенийСодержание книги
Поиск на нашем сайте
Аксонометрическое проецирование обладает простотой построения изображения и его наглядностью. «Аксонометрия» - с греческого языка означает «измерение по осям». Суть этого метода проецирования (рис. 10.1): объект относят к некоторой системе координат, а затем вместе с координатной системой параллельно проецируют его на плоскость чертежа.
A
A
x A
Рис. 10.1
При аксонометрическом проецировании изображение точек на чертеже, по существу, фиксирует их положение относительно центра О принятой системы координат. Это и делает такой чертёж обратимым. Отрезки координатных осей при их проецировании на плоскость чертежа искажаются в зависимости от направления вектора проецирования по отношению к координатной системе, с одной стороны, и к плоскости чертежа, с другой. При этом угол между плоскостью чертежа и вектором проецирования может быть равен 90
K
В зависимости от соотношения коэффициентов искажения осей аксонометрические проекции могут быть: изометрические (K диметрические (K триметрические (K
В машиностроении (согласно рекомендациям ГОСТ 2.317-69) используют прямоугольную изометрию или прямоугольную диметрию.
В прямоугольной изометрии коэффициенты искажения по осям:
K Однако изометрическую проекцию строят без сокращения размеров по осям, что приводит к увеличению изображения против оригинала в 1,22 раза.
В прямоугольной диметрии коэффициенты искажения по осям:
K
При реальном построении проекций рекомендуется принимать:
K при этом изображение увеличивается против оригинала в 1,06 раза.
Расположение осей координат в изометрии приведено на рис. 10.2, а в диметрии – на рис. 10.3. Окружность в аксонометрии изображается в виде эллипса, который удобно строить с помощью параллелограмма, отображающего квадрат, описывающий окружность.
В изометрии (рис. 10.4) эллипсы на всех координатных плоскостях одинаковы между собой.
x y
Рис. 10.2
7
8 8
y
Рис. 10.3
Описанный квадрат
y Окружность на плоскости
Рис. 10.4
В диметрии (рис. 10.5) на плоскостях XY и ZY эллипсы одинаковы между собой и отличаются от эллипса на плоскости XZ.
y
Рис. 12.5
Согласно рекомендациям ГОСТа при выполнении аксонометрических чертежей принято эллипсы заменять овалами. На рис. 10.6, 10.7 и 10.8 приведены способы построения овалов на координатных плоскостях при изометрии и диметрии.
O
Рис. 10.6
y
Рис. 10.7
O
Рис. 10.8
Техника построения аксонометрического изображения сводится к умению строить следующие элементы изображаемого объекта.
1. Точки строят по их координатам.
2. Линии строят по их точкам. 2.1. Прямые линии строят по 2-м точкам или по 1-й точке и известному направлению. 2.2. Кривые линии строят по многим точкам, достаточным для их качественного воспроизведения.
Примечание. Окружности, трансформируемые на чертеже в эллипс, строят с помощью овалов. Для того чтобы при построении аксонометрии иметь координаты точек изображаемого объекта (детали), предварительно строят обычный двух картинный чертёж детали и условно привязывают к ней систему координат.
Закрытые поверхности детали условно раскрывают путём выреза её части 2-мя взаимно перпендикулярными (координатными) плоскостями.
На рис. 10.9 приведён пример построения изометрии полой цилиндрической детали (втулки).
O z
Рис. 10.9
Библиографический список
1. Бубенников А.В. Начертательная геометрия, М., Высшая школа, 1985. 2. Фролов С.А. Начертательная геометрия, М., Машиностроение, 1983. 3. Посвянский А.Д. Краткий курс начертательной геометрии, М., Высшая школа, 1974. 4. Локтев О.В., Глазунова И.М. Краткий курс начертательной геометрии, М., Высшая школа, 1985.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 274; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.82.168 (0.008 с.) |


 z
z 



 z O
z O 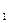



 A
A 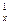 y
y 


 A A
A A 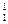

 x
x 
 O
O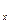

 (прямоугольная аксонометрия) или не равен 90
(прямоугольная аксонометрия) или не равен 90  ; K
; K  =
=  ; K
; K 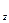 =
=  .
. K
K 
 z
z
 120
120 



 z
z







 1
1
 x 41
x 41 


 z
z







 x
x


 x y
x y
 Точки эллипса Точки эллипса
Точки эллипса Точки эллипса

 z z
z z




 x x
x x



 y
y z
z



 O
O 

 O
O 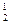


 O
O 
 x y
x y
 z
z

 O
O  O
O 

 x
x


 z
z


 O
O 
 x
x y
y
 z
z 






 O
O 
 x
x 









 y
y

 x
x


