
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение по чертежу принадлежности плоскойСодержание книги
Поиск на нашем сайте Поверхности её элементов
Процесс определения принадлежности связан с решением позиционных задач второго типа (ПЗ.2). На чертеже точку и линию, принадлежащих поверхности, можно задать (определить), только связав их с другими элементами этой поверхности, изображёнными на чертеже.
Правила определения принадлежности
1.Точка принадлежит плоскости, если она принадлежит какой-либо прямой линии этой плоскости. 2.Линия принадлежит плоскости, если она проходит через соответствующие точки этой плоскости. Точек должно быть достаточно для вычерчивания проекций рассматриваемой линии (например, прямая должна проходить через две точки этой плоскости или через одну точку, но в известном направлении).
Пример (рис. 5.20). Построить недостающие проекции точек M
a
Рис. 5.20
Алгоритм решения
1. M 2. D 3. D Определение по чертежу взаимного положения Плоскостей и прямых линий
Определение взаимного положениягеометрических фигур на чертеже связан с решением позиционных задач.
Параллельные прямая и плоскость на чертеже
Признак: прямая параллельна заданной плоскости, если она параллельна одной из прямых этой плоскости. Пример (рис. 5.21). Через точку M провести прямую a ||
a
C
B
Рис. 5.21
Алгоритм решения 1. a 2. a Параллельные плоскости на чертеже Признак: плоскости параллельны, если две пересекающиеся прямые одной плоскости параллельны соответствующим двум пересекающимся прямым другой плоскости.
Пример (рис. 5.22). Через точку М провести плоскость
Алгоритм решения: 1. 2. M 3. M
B
B a b
Рис. 5.22
Пересечение плоской поверхности с прямой Линией на чертеже
Определение результатов пересечения геометрических фигур на чертеже связано с решением позиционных задач третьего типа, получивших название «главные позиционные задачи» – ГПЗ. В зависимости от типа пересекающихся фигур различают две группы ГПЗ.
1. Задачи на пересечение поверхностей с прямыми линиями: 1.ГПЗ. Результаты пересечения – точки.
2. Задачи на пересечение поверхностей между собой: 2.ГПЗ. Результаты пересечения – прямые линии.
Различают ГПЗ с тремя возможными вариантами расположения геометрических фигур относительно основных плоскостей проекций: ГПЗ.1 - обе пересекающиеся геометрические фигуры занимают проецирующее положение ( ГПЗ.2 - одна из пересекающихся фигур занимает проецирующее, а другая - общее положение ( ГПЗ.3 - обе пересекающиеся фигуры занимают общее положение (не
Для каждого варианта и разновидности ГПЗ разработан свой типовой порядок (алгоритм) решения задач. В данном разделе рассматриваются задачи на пересечение прямой линии с плоской поверхностью (1.ГПЗ).
Решение задач 1.ГПЗ. 1 (
Алгоритм решения 1.Искомые проекции точек пересечения проецирующих геометрических фигур уже изображены на чертеже по принадлежности их главным проекциям. 2.Определяют (при необходимости) видимость элементов геометрических фигур. Пример (рис. 5.25). На трёх картинном чертеже определить проекции точки пересечения прямой a с плоскостью грани
P
a
B
Рис. 5.25
Алгоритм решения 1.a 2. 3. P
Решение задач 1.ГПЗ. 2 (
Алгоритм решения
1.Одна из искомых проекций точки пересечения геометрических фигур уже изображена на чертеже по её принадлежности главной проекции проецирующей фигуры. 2.Вторую проекцию строят по признаку её принадлежности геометрической фигуре общего положения. 3.Определяют видимость элементов заданных фигур. Пример 1 (рис. 5.26). Определить проекции точки пересечения прямой а с плоскостью грани
P a
Рис. 5.26
Алгоритм решения 1. 2. P
Пример 2 (рис. 5.27). Определить проекции точек пересечения прямой а с пирамидой
Алгоритм решения 1. a 2. P 3. P
S
P
A m
Рис. 5.27
Решение задач 1.ГПЗ. 3 (не
Эти главные позиционные задачи решают с использованием метода введения дополнительной (вспомогательной) плоскости – посредника.
Алгоритм решения 1. Заданную прямую заключают во вспомогательную проецирующую плоскость – посредник. 2. Строят линию пересечения заданной поверхности с плоскостью – посредником. 3. Определяют точку (точки) пересечения заданной прямой с полученной линией, которая и является искомым решением задачи. 4. Определяют видимость элементов заданных геометрических фигур.
Пример (рис. 5.28). Определить точку пересечения прямой а с плоскостью общего положения
Алгоритм решения 1. a 2. 3. a
1 m a C Рис. 8.28
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 и D
и D  , расположенных в плоскости треугольника
, расположенных в плоскости треугольника  (ABC). Провести через точку D в плоскости заданного треугольника прямую a || AB.
(ABC). Провести через точку D в плоскости заданного треугольника прямую a || AB. C
C 









 M
M  B
B 

 1
1 

 A
A 
 D
D 

 C
C 
 M
M  C
C  ;
; .
.


 B
B 

 A
A  C
C 
 M
M 
 A
A  (a || b).
(a || b). h
h 
 a;
a;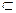 h || h
h || h 

 a
a 




 A
A 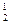 h
h  M
M 


 A
A 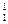 h
h  ,
, 






 a
a 



 C
C 




 B
B 


 A
A 


 A
A 





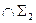 ;
;


 a
a  B
B 

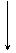 A
A 



 A
A 
 C
C 
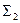

 ;
;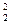 = a
= a 







 n
n 



 a
a 

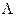

 A
A 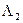 = m
= m 



 2
2 
 1
1 



 C
C 


 2
2 
 A
A 
 P
P 



