
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Взаимное пересечение кривых поверхностейСодержание книги
Поиск на нашем сайте На чертеже (2.ГПЗ)
Решение задач 2.ГПЗ. 1 (
Алгоритм решения 1.Искомые проекции линии пересечения проецирующих геометрических фигур уже изображены на чертеже по принадлежности их главным проекциям. 2.Определяют видимость элементов геометрических фигур. Пример. Рассмотреть варианты пересечения кривых поверхностей на базе проецирующих цилиндров вращения. Результатом пересечения, в общем случае, являются пространственные кривые линии 4-го порядка (описываются уравнениями 4-го порядка). Вариант 1 (рис. 6.36). Результат пересечения – проницание: m
Рис. 6.36
Вариант 2 (рис. 6.37). Результат пересечения – вмятие: n =
n
Рис. 6.37
Вариант 3 (рис. 6.38). Результат пересечения – проницание с касанием: k =
Рис. 6.38
Решение задач 2.ГПЗ. 2 (
Алгоритм решения:
1.Одна из искомых проекций линии пересечения геометрических фигур уже изображена на чертеже по её принадлежности главной проекции проецирующей фигуры. 2.Вторую проекцию строят по признаку её принадлежности геометрической фигуре общего положения. 3.Определяют видимость элементов заданных фигур.
Пример (рис. 6.39). Построить проекции линии проницания с касанием m при пересечении сферы
Алгоритм решения
1. m 2. На профильной проекции линии пересечения фигур выбираем несколько её точек. Строим их фронтальные проекции (по принадлежности точек сфере). Через построенные проекции точек проводим кривую линию (с учётом видимости её частей), являющейся проекцией m
Рис. 6.39
Решение задач 2.ГПЗ. 3 (не
Эти главные позиционные задачи решают, применяя дополнительные построения. Чаще всего используют при этом метод введения дополнительных плоскостей – посредников.
Алгоритм решения
1.Строят вспомогательную проецирующую плоскость - посредник так, чтобы она пересекала обе заданные геометрические фигуры (поверхности).
2.Определяют обе линии пересечения посредника с заданными поверхностями, т.е. решают две задачи 2. ГПЗ. 2.
3.Определяют точки пересечения построенных линий. Эти точки - общие для заданных геометрических фигур.
4.Для получения достаточного числа общих точек пересекающихся фигур определяют и строят необходимое количество посредников. По полученным точкам строят искомую линию пересечения.
5.Определяют видимость элементов заданных геометрических фигур.
В данном разделе рассматривается порядок расчёта 2.ГПЗ.3 с пересекающимися поверхностями вращения. Степень сложности решения этих задач зависит от взаимного положения осей вращения пересекающихся поверхностей.
Возможны следующие четыре варианта взаимного положения осей: 1.Оси вращения поверхностей совпадают: i
2.Оси параллельны: i
3.Оси пересекаются: i
4.Оси вращения являются скрещивающимися прямыми: i
Рассмотрим примеры решения некоторых задач
Пример 1 (рис. 6.40). Построить линию пересечения m полусферы
n
Рис. 6.40
Решение
Линиями пересечения таких поверхностей являются общие параллели, т.е. траектории вращения общих точек образующих заданных поверхностей.
Пример 2 (рис. 6.41). Построить линию пересечения полусфер
Рис. 6.41
Решение
Задачу решаем с использованием дополнительных проецирующих плоскостей - посредников, перпендикулярных осям вращения заданных полусфер. При этом задача сводится к решению нескольких задач типа 2.ГПЗ.2. Плоскости - посредники рассекают заданные поверхности по параллелям. Точки пересечения параллелей являются искомыми общими точками заданных поверхностей. Через построенные точки проводим искомую линию пересечения заданных поверхностей – окружность n.
Пример 3 (рис. 6.42). Построить линию пересечения конуса
i
Рис. 6.42
Решение
Для решения подобных задач вместо проецирующих плоскостей-посредников рациональнее использовать концентрические секущие сферы-посредники с центрами в точке пересечения осей вращения заданных поверхностей. Концентрические сферы пересекают заданные фигуры по параллелям - окружностям. При этом задача сводится к решению нескольких задач с поверхностями вращения, у которых совпадают оси вращения (смотри ранее рассмотренный Пример 1). Точки пересечения построенных параллелей являются искомыми общими точками заданных фигур: точками линии их пересечения.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 ,
, 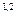 =
=  .
.

 m
m 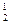
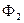 m
m 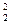
 = m
= m 












 k
k 
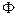 с цилиндром вращения
с цилиндром вращения 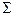 , если
, если  .
. .
.

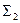 m
m 


 = i
= i  .
. i
i  i
i 

 m
m 

 n
n 

 m
m 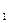














 = m
= m 





 n
n 


 m
m  m
m 






 P
P 
 m
m 




