
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кривые поверхности с прямолинейными образующимиСодержание книги
Поиск на нашем сайте
(линейчатые поверхности)
1.1. Цилиндрическаяповерхность
Цилиндрическая поверхность моделируется параллельным движением образующей прямой по направляющей кривой (плоской или пространственной). На рис. 6.3а представлен её аксонометрический чертёж, на рис. 6.3б – комплексный чертёж определителя этой поверхности, а на рис. 6.3в – чертёж самой поверхности.
l
m
Рис. 6.3
Частный случай цилиндрической поверхности - цилиндрвращения (рис. 6.4), у которого направляющая – замкнутая кривая линия – окружность m, при этом образующая l
Рис. 6.4
1.2. Коническаяповерхность
Коническая поверхность моделируется образующей прямой, проходящей через общую точку (вершину) и перемещающейся по направляющей кривой (плоской или пространственной).
Рис. 6.5
Аксонометрический чертёж такой поверхности представлен на рис.6.5а, комплексный чертёж её определителя – на рис. 6.5б, чертёж очерка конической поверхности – на рис. 6.5в. Частный случай конической поверхности – конус вращения (рис. 6.6).
S
Рис 6.6
1.3. Поверхности вращения с прямолинейными образующими
В зависимости от взаимного положения образующей и оси вращения различают следующие варианты поверхностей. 1. Цилиндрвращения 2. Конусвращения 3. Однополостныйгиперболоидвращения
Рис. 6.7

i
Рис. 6.8
i
а) Чертёж определителя однополостного б) Очерковый чертёж поверхно- гиперболоида вращения
Рис. 6.9 1.5. Винтовые поверхности с прямолинейными образующими (геликоиды)
Эти поверхности моделируют винтовым движением образующей, пересекающей направляющие: винтовую линию и ось вращения. Образующая совершает при этом сложное движение: вращательное вокруг оси и поступательное вдоль оси, одновременно.
Если угол между образующей и осью вращения равен 90 Если угол между образующей и осью вращения не равен 90 На рис. 6.10 приведён чертёж элементов определителя косого геликоида и его конус параллелизма Винтовые поверхности используют при образовании резьбовых поверхностей деталей машин.
l i
Рис. 6.10
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 278; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.163.142 (0.008 с.) |


 а)
а)

 l
l






 m
m
 б) в)
б) в)




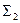

 m
m 



 l
l 




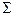 (m).
(m).


 l
l 






 m
m  = m
= m 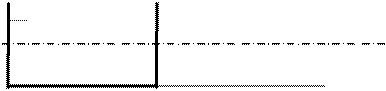




 а) l S
а) l S








 б) S
б) S  l
l 







 m
m 





 l
l 

 S
S 


 m
m  i), см. рис. 6.8.
i), см. рис. 6.8. i), см. рис. 6.9.
i), см. рис. 6.9.


 l
l 

 i
i 


 l
l 

 S
S 


 l
l 


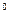 , то при моделировании получают прямой геликоид, у которого имеется плоскость параллелизма, перпендикулярная оси вращения. Все образующие прямого геликоида параллельны этой плоскости.
, то при моделировании получают прямой геликоид, у которого имеется плоскость параллелизма, перпендикулярная оси вращения. Все образующие прямого геликоида параллельны этой плоскости. .
.
 l
l 













