
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Особенности решения задач на пересечениеСодержание книги
Поиск на нашем сайте
поверхностей вращения, описанных вокруг сферы (теорема Г. Монжа)
Две поверхности вращения второго порядка в общем случае пересекаются по пространственной кривой четвёртого порядка. Однако в некоторых частных случаях эти кривые выраждаются в плоские кривые линии второго порядка. Известный французский геометр Г. Монж доказал следующую теорему: Если две поверхности вращения описаны вокруг сферы, то результатом их взаимного пересечения являются две плоские кривые второго порядка. Пример (рис. 6.43). Построить фронтальные проекции линий пересечения двух цилиндров
Рис. 6.43
Решение Плоскости кривых линий пересечения фигур m
Вопросы для самоконтроля
1. Назвать основные разновидности кривых поверхностей.
2. Какие правила используют при построении точек или линий заданной кривой поверхности?
3. Назвать порядок решения задач (алгоритм) – 1.ГПЗ с кривыми поверхностями.
4. Назвать порядок решения задач (алгоритм) – 2.ГПЗ с кривыми поверхностями.
5. Какие виды линий можно получить, пересекая цилиндр вращения плоскостью?
6. Какие виды линий можно получить, пересекая конус вращения плоскостью?
7. В чём смысл теоремы Г.Монжа о пересечении поверхностей вращения?
7. Решение задач с преобразованием чертежа
Любые графические задачи (позиционные, метрические, комплексные) значительно упрощаются, если геометрические фигуры занимают частное положение относительно плоскостей проекций, т.е. они или параллельны, или перпендикулярны им. Такое положение фигур позволяет сразу получить на чертеже требуемое решение, поэтому его называют решающимположением.
Например, истинная величина отрезка определится сразу по чертежу, если отрезок займёт положение прямой уровня. Чтобы получить решающее положение фигуры, чертёж преобразовывают, строя новые (дополнительные) проекции фигуры на основе имеющихся проекций.
Применяют следующие способы преобразования чертежа.
1. Вращение заданной фигуры вокруг проецирующей оси (рис. 7.1).
A
Рис. 7.1
2. Вращение фигуры вокруг прямой уровня (рис. 7.2).
A
ив |AB| f A
Рис. 7.2
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.251.204 (0.009 с.) |

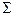 и
и 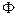 , описанных вокруг сферы
, описанных вокруг сферы 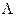 .
.



 C
C  D
D 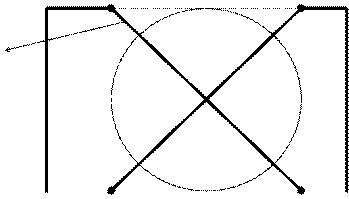
 m
m 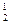 A
A 
 m
m 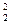





 F
F 
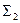
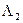
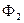
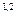 проходят через прямую, соединяющую точки двойного соприкосновения. Точками двойного соприкосновения называют 2 точки, в которых сфера одновременно касается обеих поверхностей. В нашем случае точками двойного соприкосновения являются точки А и В. Они определяются как точки пересечения окружностей a
проходят через прямую, соединяющую точки двойного соприкосновения. Точками двойного соприкосновения называют 2 точки, в которых сфера одновременно касается обеих поверхностей. В нашем случае точками двойного соприкосновения являются точки А и В. Они определяются как точки пересечения окружностей a 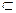


 и.в. |AB| B
и.в. |AB| B 
 A
A 
 A
A 


 A
A 


 B
B  3. Введение новых, дополнительных плоскостей проекций, ортогональных к уже используемым в чертеже плоскостям проекций и относительно которых рассматриваемая геометрическая фигура займёт решающее положение.
3. Введение новых, дополнительных плоскостей проекций, ортогональных к уже используемым в чертеже плоскостям проекций и относительно которых рассматриваемая геометрическая фигура займёт решающее положение.


 и.в. |AB| B
и.в. |AB| B 

 f
f 
 A
A 



 A
A  C
C 

 B
B 




