Поверхности вращения с криволинейной образующей

Рассмотрим такую поверхность общего вида (рис. 6.11), для которой в качестве образующей линии взята плоская кривая линия, при этом плоскость этой образующей проходит через ось вращения. Обратим внимание на то, что при вращении образующей линии l каждая её точка описывает траекторию в виде окружности. Для удобства описания построения поверхности и решения с ней задач вводят собственные названия для некоторых линий поверхности:

1. Параллель a – траекторная окружность какой-либо точки образующей l.

2. Экватор b – параллель с наибольшим радиусом.

3. Горло c – параллель с наименьшим радиусом.

4. Меридиан l – линия пересечения осевой плоскости с поверхностью (в примере – образующая линия). Главный меридиан - меридиан, лежащий в плоскости, параллельной какой-либо основной плоскости проекций.

Примечание: при изображении таких поверхностей удобно располагать их так, чтобы относительно основных плоскостей проекций ось вращения занимала проецирующее положение.

 

l i l

 

 

l

 

 

i a b

c

 

а) Чертёж определителя б) Чертёж поверхности .

поверхности (l, i).

 

Рис. 6.11

 

Частные разновидности поверхностей вращения

Это поверхности, получаемые вращением плоской кривой образующей второго порядка (окружности, эллипса, параболы и гиперболы) вокруг оси, лежащей в плоскости образующей кривой.

 

1. Тороваяповерхность

Торовая поверхность моделируется вращением вокруг оси образующей окружности или её дуги.

 

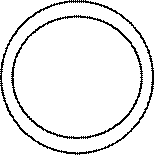
Разновидности торовых поверхностей:

1.1. Сфера (m, i = d), представленная на рис. 6.12.

 

l i i = l i i

 

 

Рис. 6.12

 

1.2. Кольцо (m, i d), см. рис. 6.13.

i i

l

 

 

 

 

l

i

 

 

а) Чертёж элементов определителя б) Очерковый чертёж кольца

торового кольца

Рис. 6.13

 

1.3. Галтель (m, i), см. рис. 6.14.

 

 

l l

 

 

i

i

 

 

 

Рис. 6.14

 

2. Эллипсоидвращения

 

Эллипсоид вращения моделируется вращением вокруг своей оси образующего эллипса. Различают 2 вида эллипсоида:

 

2.1. Сжатый эллипсоид (m, i), см. рис. 6.15.

 

i i

 

 

Рис. 6.15

 

2.2. Вытянутый эллипсоид (m, i), см. рис. 6.16.

 

i i

 

Рис. 6.16

 

3. Параболоид вращения

 

Параболоид вращения (рис. 6.17), моделируется вращением образующей параболой вокруг её оси.

 

 

i i

 

 

Рис. 6.17

 

4. Гиперболоид вращения

 

Различают:

4.1.Однополостный гиперболоид вращения (l, i), у которого образующая гипербола l вращается вокруг её действительной оси (рис. 6.18).

 

i

 

l

 

 

 

l i

 

 

Рис. 6.18

 

4.2. Двухполостный гиперболоид вращения (m, i), у которого образующая гипербола вращается вокруг её мнимой оси (рис. 6.19).

 

l l

 

i i

= ()

Рис. 6.19

 

Каналовые поверхности

 

Эти поверхности моделируются замкнутым плоским контуром (прямолинейным или криволинейным), который перемещается своим центром по направляющей линии. При этом угол между направляющей и плоскостью образующего контура остаётся постоянным (например, 90 ). Образующий контур при перемещении может оставаться неизменным или изменять свои размеры, оставаясь подобным исходному контуру.

Чертёж такой поверхности представлен на рис. 6.20.

 

 

 

 

Рис. 6.20

 

 

Каналовые поверхности с неизменным образующим контуром называют трубчатыми (рис. 6.21).

 

 

 

 

 

 

 

Рис. 6.21

 

Частным случаем каналовых поверхностей являются циклические каналовые поверхности, у которых образующим контуром является окружность или эллипс (рис. 6.22).

 

 

 

 

 

Рис. 6.22