
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решающие положения прямых линий и плоскостейСодержание книги
Поиск на нашем сайте
На чертеже
Решающие положения для прямых линий
Вариант 1 (рис. 7.3). Преобразовать чертёж так, чтобы прямая общего положения стала прямой уровня. Это положение прямой используется для определения по чертежу истинной величины её отрезка или угла её наклона к плоскости проекций.
2k h B
Рис. 7.3
Вариант 2. Преобразовать чертёж так, чтобы прямая линия общего положения стала проецирующей прямой. Это положение прямой линии используется для определения следующих мерных величин геометрических фигур.
1. Расстояние между прямой и точкой – отрезок MK (рис. 7.4).
a
K
Рис. 7.4
2. Расстояние между параллельными прямыми – отрезок MK (рис. 7.5).
a
f
Рис. 7.5
3. Расстояние между скрещивающимися прямыми линиями – отрезок MK (рис. 7.6).
b
a
Рис. 7.6
4. Величина гранных углов (рис. 7.7).
Рис. 7.7
Решающие положения для плоскостей
Вариант 1. Преобразовать чертёж так, чтобы плоскость общего положения стала проецирующей. Это положение заданной плоскости позволяет определять следующие мерные величины геометрических фигур.
1. Расстояние от точки до плоскости – отрезок MK (рис. 7.8)
M
Рис. 7.8
2. Расстояние между параллельными плоскостью и прямой – отрезок MK (рис. 7.9).
K
Рис. 7.9
3. Расстояние между параллельными плоскостями – отрезок MK (рис. 7.10).
K
Рис. 7.10
4. Величина гранных углов (рис. 7.11).
Рис. 7.11
5. Углы наклона заданной плоскости к плоскостям проекций (рис. 7.12).
Рис. 7.12
Вариант 2 (рис. 7.13). Преобразовать чертёж так, чтобы плоскость общего положения стала плоскостью уровня.
Это положение плоскости позволяет определять истинную величину плоских фигур (граней) и их площадь.
Рис. 7.13
7.2. Преобразование чертежа методом введения дополнительных ортогональных плоскостей проекций
Сущность данного способа состоит в том, что заданные геометрические фигуры сохраняют своё положение в пространстве относительно принятой (основной) системы ортогональных плоскостей проекций. Но при этом вводятся новые (дополнительные) ортогональные плоскости проекций так, чтобы в новой паре взаимно перпендикулярных плоскостей проекций заданные фигуры располагались бы уже частным образом, наиболее удобным для решения поставленной задачи: геометрические фигуры занимали бы решающее положение.
Пример 1 (рис. 7.14). Задан чертёж отрезка прямой общего положения АВ. Требуется:
1) определить истинную длину этого отрезка и угол его наклона к горизонтальной плоскости проекций (угол
2) определить расстояние от заданной точки М до прямой АВ.
A
Рис. 7.14
Решение первой задачи Прямое решение первой задачи методом прямоугольного треугольника ранее нами уже было рассмотрено. Теперь решим эту задачу путём введения дополнительной плоскости проекций
Решение второй задачи Решающим положением заданных элементов будет такое, когда отрезок АВ станет проецирующим относительно дополнительной плоскости
Пример 2 (рис 7.15). Задан чертёж треугольной грани АВС общего положения и точка М вне грани. Требуется: 1) построить перпендикуляр МК к плоскости 2) определить площадь треугольника АВС. Решение первой задачи Решающим положением будет такое, когда плоскость
A
B Рис. 7.15
Для построения на чертеже дополнительной плоскости
Решение второй задачи Решающим положением для неё будет, когда плоскость Далее, проводим новую плоскость проекций:
Вопросы для самоконтроля
1. В чём принцип преобразования чертежа методом вращения заданной геометрической фигуры вокруг проецирующей оси? 2. В чём принцип преобразования чертежа методом вращения заданной геометрической фигуры вокруг прямой уровня? 3. В чём принцип преобразования чертежа методом введения дополнительных плоскостей проекций? 4. Какие решающие положения можно получить для прямых линий общего положения, преобразуя чертёж, какие задачи при этом становятся решёнными? 5. Какие решающие положения можно получить для плоскостей общего положения, преобразуя чертёж, какие задачи при этом становятся решёнными?
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 240; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.68.25 (0.006 с.) |

 A
A  h
h 

 1k
1k
 A
A 


 f
f 



 a
a 
 M
M 

 f
f 


 a
a  K
K  a
a 





 M
M 
 f
f 

 M
M  K
K 
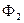
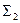



 и.в. |
и.в. |  |
|

 l
l 

 l
l 




 K
K 






 f
f  M
M 

 K
K 






 f
f 

 K
K 


 ||
|| 

 M
M 
 f
f 




 и.в. |
и.в. | 



















 и.в. |
и.в. | 


 M
M  A
A 





 B
B 
 A
A 

 M
M 











 K
K  = B
= B 

 M
M  M
M 

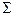 (АВС) и определить его величину;
(АВС) и определить его величину;



 ив |MK|
ив |MK|












 M
M 



 f
f 









 M
M 



