
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства проекций кривых линийСодержание книги
Поиск на нашем сайте
1. Если точка принадлежит кривой линии, то проекции этой точки принадлежат проекциям кривой.
2. Секущая и касательная к плоской кривой проецируются соответственно в секущую и касательную к проекции кривой.
3. Плоская кривая проецируется в линию того же порядка. Например, проекция окружности – эллипс или окружность, проекция параболы – парабола.
Вопросы для самоконтроля 1. Каким способом можно отличить на чертеже плоскую кривую линию от пространственной? 2. Объяснить характер моделирования цилиндрической винтовой линии. 3. Объяснить метод построения овала. 4. Назвать основные свойства проекций кривых линий.
Плоские поверхности на чертеже
Любая поверхность (геометрическая фигура) создаётся в нашем воображении траекторным способом: поверхность моделируется путём непрерывного перемещения в пространстве некоторой линии, которая, в общем случае, может менять свою форму. Эту линию, производящую поверхность, называют образующей. Многообразие поверхностей зависит как от вида образующей, так и от закона её перемещения, который графически задаётся определёнными линиями - направляющими. Совокупность элементов моделирования поверхности, обеспечивающая закон её образования, называют определителем поверхности. Например, записывают: плоскость Все поверхности (геометрические фигуры) условно разделяют на два вида: плоские и кривые. В этом разделе рассматриваются плоские поверхности.
Разновидности плоских поверхностей
Различают простые и составные плоские поверхности.
Простые плоские поверхности бывают двух видов: плоскости и грани.
Плоскость – неограниченная плоская поверхность. На чертеже плоскость задают изображением элементов её определителя. Плоскость моделируют как траекторию непрерывного перемещения прямой образующей. Перемещение образующей можно задавать следующим образом.
1). Параллельными прямыми – 2). Двумя пересекающимися прямыми – 3). Вращением вокруг оси, перпендикулярной образующей прямой, – 4). Точкой и прямой –
Грань – плоскость, ограниченная замкнутой линией. На чертеже грань изображают линиями её границ (контуром, очерком).
На рис. 5.1 – 5.3 представлены изображения граней: треугольника, четырёхугольника и круга.
B
Рис. 5.1
Рис. 5.2
Рис. 5.3
Составные плоские поверхности (многогранные) – представляют собой несколько граней (не лежащих в одной плоскости), состыкованных между собой. Линию стыка каждой пары граней называют рёбром, которое является общей линией границ этих граней (их общей образующей).
Составные плоские поверхности подразделяют на монотипные и комплексные многогранные поверхности.
Монотипные многогранные поверхности моделируют с помощью направляющей ломаной прямой линии. При этом различают следующие варианты таких поверхностей.
1. Призматическая поверхность. Моделирование призматической поверхности производят путём параллельного перемещения образующей прямой l по направляющей ломаной прямой m (все рёбра между собой параллельны). На рис. 5.4 представлен аксонометрический чертёж призматической поверхности.
Рис. 5.4
Комплексный чертёж определителя призматической поверхности представлен на рис. 5.5.
m
Рис. 5.5 Комплексный чертёж призматической поверхности выполнен на рис. 5.6.
Рис. 5.6
Частным случаем призматической поверхности является призма, которая представляет собой замкнутую призматическую поверхность (направляющая ломаная прямая – замкнута). На рис. 5.7 приведён чертёж прямой трёхгранной призмы.
Рис. 5.7
2. Пирамидальная поверхность – моделируется перемещением прямой образующей l по ломаной направляющей прямой m, когда другой её конец остаётся в точке S – вершине призматической поверхности (все рёбра пересекаются в одной точке). На рис. 5.8 представлен комплексный чертёж двухгранной пирамидальной поверхности.
m Рис. 5.8
Частным случаем пирамидальной поверхности является пирамида, которая представляет собой замкнутую пирамидальную поверхность (направляющая ломаная прямая – замкнута). На рис. 5.9 представлен комплексный чертёж трёхгранной прямой пирамиды.
Рис.5.9 Комплексные многогранные поверхности получают стыковкой граней и многогранных поверхностей разного типа. Примером такой поверхности может служить поверхность октаэдра.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

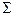 (l, a || b). Здесь в скобках записан определитель поверхности, где указаны параллельные направляющие параллельные прямые a и b, по которым перемещается прямая линия l, образуя поверхность
(l, a || b). Здесь в скобках записан определитель поверхности, где указаны параллельные направляющие параллельные прямые a и b, по которым перемещается прямая линия l, образуя поверхность  b).
b). i).
i).



 C
C  C
C 

 A
A 




















 l
l
 m
m


 l
l 



 m
m 



 l
l 



















 S
S 








 S
S 







 S
S 







 S
S 


