
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пересечение кривой поверхности с плоскостьюСодержание книги
Поиск на нашем сайте
На чертеже (2.ГПЗ) Решение задач 2.ГПЗ. 1 (
Алгоритм решения 1.Искомые проекции линии пересечения проецирующих геометрических фигур уже изображены на чертеже по принадлежности их главным проекциям. 2.Определяют видимость элементов геометрических фигур.
Пример. Определить возможные варианты линий пересечения цилиндра вращения Возможны три варианта линий пересечения. Вариант 1 (рис 6.27). Заданная плоскость
i
k
Рис. 6.27
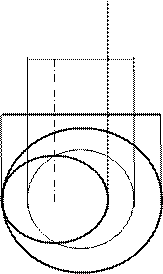
Вариант 2 (рис. 6.28). Заданная плоскость
i
Рис. 6.28
Вариант 3 (рис. 6.29). Заданная плоскость
i

Рис. 6.29
Решение задач 2.ГПЗ. 2 (
Алгоритм решения тот же, что и при решении задач на пересечение плоских поверхностей:
1.Одна из искомых проекций линии пересечения геометрических фигур уже изображена на чертеже по её принадлежности главной проекции проецирующей фигуры. 2.Вторую проекцию строят по признаку её принадлежности геометрической фигуре общего положения. 3.Определяют видимость элементов заданных фигур.
Пример. Построить возможные варианты линий пересечения конуса вращения
Вариантов линий – пять. Вариант 1 (рис. 6.30).
Рис. 6.30 Вариант 2 (рис. 6.31).
Рис. 6.31
Вариант 3 (рис. 6.32).
Рис. 6.32 Вариант 4 (рис. 6.33).
m
Рис. 6.33 Вариант 5 (рис. 6.34).
Рис. 6.34
Решение задач 2.ГПЗ. 3 (не
Эти главные позиционные задачи решают, как и при решении задач на пересечение плоских поверхностей, с использованием метода введения дополнительных плоскостей – посредников.
Алгоритм решения
1.Строят вспомогательную проецирующую плоскость - посредник так, чтобы она пересекла обе заданные геометрические фигуры (поверхности). 2.Определяют обе линии пересечения посредника с заданными геометрическими фигурами, т.е. решают две задачи 2. ГПЗ. 2. 3.Определяют точки пересечения построенных линий. Эти точки - общие для заданных геометрических фигур. 4.Для получения достаточного числа общих точек пересекающихся фигур определяют и строят необходимое количество посредников. По полученным точкам строят проекции искомой линии пересечения. 5.Определяют видимость элементов заданных геометрических фигур.
Пример (рис. 6.35). Определить и построить линию пересечения конуса вращения
P
Рис. 6.35 Решение 1. Результат пересечения: плоская кривая – эллипс. 2. Выбираем первую плоскость - посредник 3. Проводя ещё несколько плоскостей-посредников, по полученным точкам строят линию пересечения - эллипс. 4. Определяется видимость элементов грани и конуса.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 ,
,  с плоскостью
с плоскостью  . Принять, что геометрические фигуры занимают проецирующее положение.
. Принять, что геометрические фигуры занимают проецирующее положение. =
=  - прямые линии.
- прямые линии.

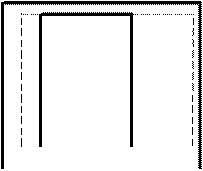


 k
k 
 k
k 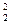






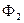

 i
i 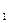






 k
k 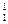






 i
i 



 l,
l, 





 = n
= n 


 i
i 

 S.Результат пересечения – прямые образующие l
S.Результат пересечения – прямые образующие l  и l
и l  .
.




 l
l 








 =l
=l  l
l 




 m
m 
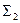













 n
n 




 m
m 



 ,
, 










 n
n 





 ) l
) l 
 P
P 














 P
P  = l
= l  ||
|| 
 , которая проходит через ось эллипса пересечения и его образующую l. Получаем точку эллипса P
, которая проходит через ось эллипса пересечения и его образующую l. Получаем точку эллипса P  . В примере графическое решение закончено на этом этапе.
. В примере графическое решение закончено на этом этапе.


