
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Относительно основных плоскостей проекцийСодержание книги
Поиск на нашем сайте
По расположению рассматриваемых плоскостей относительно основных плоскостей проекций различают плоскости частного и общего положения. Плоскости частного положения разделяют на следующие два типа. 1. Проецирующая плоскость, перпендикулярная какой-либо из основных плоскостей проекций. 2. Плоскость уровня, параллельная какой-либо плоскости проекций. Проецирующая плоскость на перпендикулярной ей плоскости проекций изображается в виде прямой линии, т.е. геометрической фигурой на единицу меньшего измерения. Эту проекцию принято называть главной проекцией проецирующей плоскости. Здесь же без искажения изображены и углы её наклона к другим плоскостям проекций.
Среди проецирующих плоскостей различают следующие плоскости.
1. Горизонтально проецирующая плоскость (рис. 5.10).
Рис. 5.10
2. Фронтально проецирующая плоскость (рис. 5.11). 3. Профильно проецирующая плоскость (рис. 5.12).
Рис. 5.11
Рис. 5.12
Среди плоскостей уровня различают следующие плоскости. 1. Горизонтальная плоскость (рис. 5.13).
Рис.5.13 2. Фронтальная плоскость (рис. 5.14).
Рис. 5.14
3. Профильная плоскость (рис. 5.15).
Рис. 5.15
Проекция плоскости уровня на плоскость проекций, которой она не параллельна (а, следовательно, перпендикулярна), изображается прямой, перпендикулярной линиям связи с параллельной плоскостью проекций. Эту проекцию принято называть главной и определяющей. На плоскости проекций, которой параллельна грань, определены истинная форма грани и её площадь.
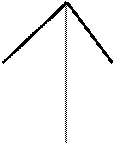
Плоскости общего положения (относительно основных плоскостей проекций) на чертеже изображаются с искажением их метрических параметров (например, длин отрезков, углов их наклона к плоскостям проекций) и для определения этих параметров требуются дополнительные построения. Например, если необходимо определить угол наклона заданной плоскости общего положения
g
g
Рис. 5.18
Эту прямую обозначают буквой g Теперь, если на прямой g Для определения углов наклона плоскости
Решим задачу (рис. 5.17). Через точку В
Алгоритм решения
1.В 2.g 3.Угол первого катета B
и.в. |BD| 1k D g
Рис. 5.19
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 353; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.006 с.) |






























 (и.в.)
(и.в.)





 (рис. 5.16) к плоскости проекций
(рис. 5.16) к плоскости проекций  (угол
(угол 















 и
и  ) на заданной плоскости строят соответствующие прямые линии наклона g
) на заданной плоскости строят соответствующие прямые линии наклона g  и g
и g  , которые перпендикулярны соответственно фронталям и профильным прямым.
, которые перпендикулярны соответственно фронталям и профильным прямым. ( ABC) провести линию наклона g
( ABC) провести линию наклона g 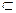 g
g  h = AC
h = AC  В
В  AC = D
AC = D 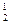 = B
= B  D
D  B
B 
 D
D 




 A
A 




 B
B 

 B
B 




 A
A 


