
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Получение обратимого чертежа,Содержание книги
Поиск на нашем сайте
задание на нём точки Следует отметить, что на рабочем чертеже рассматриваемый объект (например, точка) должен быть задан таким образом, чтобы можно было представить его пространственное положение. Для этого чертёж должен быть обратимым, т. е. содержать трёхмерную информацию об объекте. Задачу обратимости чертежа можно решить следующими двумя способами.
Способ 1. Получение обратимого чертежа путём использования аксонометрического проецирования – проецирования, при котором строят не только изображение объекта (например, точки), но и осей принятой системы координат (x, y, z), с которой условно связывают объект. На рис 2.1 представлен изометрический чертёж точек А и В. Существует множество положений плоскости чертежа относительно осей координат. Но в любом случае на чертеже координатные оси отобразятся, как пучок из трёх прямых. Если плоскость чертежа расположить так, чтобы При аксонометрическом изображении точку (объект) рассматривают относительно начала координат, определяя расстояние между ними по осям x, y, z. Эти расстояния получили название координаты заданной точки. Возможность определения по чертежу трёхмерного положения любой точки рассматриваемого объекта и делает такой чертёж обратимым.
Способ 2. Получение обратимого чертежа путём проецирования объекта не на одну, а на две взаимно перпендикулярные (ортогональные) плоскости проекций (рис. 2.2). Для этого можно использовать любую пару плоскостей, образуемых координатными осями, которые получили следующие названия и обозначения: горизонтальная плоскость проекций (x фронтальная плоскость проекций (x профильная плоскость проекций (y Эти три плоскости получили называние: основные плоскости проекций.
A
x A
Рис. 2.1
A
A
A
условный поворот плоскости
Рис. 2.2
Две основные проекции (картины) объекта можно поместить на поле (плоскости) чертежа (рис. 2.3), условно поворачивая одну из плоскостей проекций (плоскость
A
Рис. 2.3
Такой чертёж получил название «обратимый двух картинный чертёж», или «эпюр Монжа». Гаспар Монж (французский геометр) в 1798 году опубликовал первый в мире курс «Начертательная геометрия», где и развил схему построения такого чертежа. Основные плоскости проекций (с изображениями) можно разместить на плоскости чертежа, принимая одну из них в качестве базовой (главной). Остальные две плоскости проекций (картины) при этом должны располагаться в проекционной связи с базовой плоскостью проекций.
Рис. 2.4
Возможны 3 варианта размещения картин (плоскостей проекций):
1.С горизонтальной базовой плоскостью проекций (рис. 2.4). 2.С фронтальной базовой плоскостью проекций (рис. 2.5). 3.С профильной базовой плоскостью проекций (рис. 2.6).
y Рис. 2.5
A
x
Рис. 2.6
В машиностроении для выполнения чертежей принят второй вариант – с фронтальной базовой плоскостью проекций. Как уже отмечалось, для получения обратимого чертежа достаточно использовать только две плоскости проекций (картины): комплекс Если на двух картинном чертеже (рис. 2.7) изобразить проекции каких либо двух точек, (например, A и B,) то на их положение относительно друг друга не влияют ни размеры плоскостей проекций, ни границы между ними.
A
Рис. 2.7
Поэтому, контуры плоскостей проекций и их общую ось можно не изображать на чертеже. Такой чертёж получил название «безосный комплексный чертёж». При переходе к безосному чертежу теряется картина расположения заданных точек относительно системы координат, но сохраняется точность и удобство трёхмерного представления их взаимного положения при значительном упрощении изображения. При необходимости, могут использоваться комплексные безосные чертежи с числом картин больше двух. Чтобы воссоздать по чертежу реальную картину, соответствующую оригиналу (например, взаимное положение точек А и В), требуется работа воображения, требуется «прочитать» чертёж, решая позиционные задачи ПЗ.1 о взаимном положении точек (левее, правее, ближе, дальше, выше, ниже). Для удобства работы с комплексным чертежом используют линии связи проекций между собой (например, линии связи проекций A Точки, расположенные на одном проецирующем луче, называют конкурирующими. Эти точки как бы конкурируют между собой на видимость их изображения на чертеже. Понятие о конкурирующих точках вводится для определения видимости отдельных элементов фигур при рассмотрении их взаимного расположения. Различают горизонтально конкурирующие, фронтально конкурирующие и профильно конкурирующие точки. Например, горизонтально конкурирующие точки А и В (рис. 2.8) расположены на одном горизонтально проецирующем луче.
C
Рис. 2.8
На горизонтальной плоскости их проекции сливаются (A
Вопросы для самоконтроля
1. Назвать способы получения обратимого чертежа. 2. Как строится эпюр Монжа? 3. Какие возможны варианты взаимного размещения «картин» в эпюре Монжа? 4. Что представляет собой безосный комплексный чертёж? 5. Какие точки называют конкурирующими, в чём они конкурируют?
Прямые линии на чертеже
Чтобы задать положение прямой линии в пространстве (рис.3.1), достаточно задать положение любых двух её точек (А и В).
Рис. 3.1
По расположению прямых относительно основных плоскостей проекций различают прямые общего и частного положения.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 1035; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.204 (0.009 с.) |

 она имела одинаковые углы со всеми осями, то на чертеже координатные оси будут составлять между собой углы по 120
она имела одинаковые углы со всеми осями, то на чертеже координатные оси будут составлять между собой углы по 120  и иметь одинаковые коэффициенты уменьшения (искажения) своего изображения по отношению к оригиналу. Для удобства принято считать этот коэффициент равным единице. Такое аксонометрическое проецирование называют изометрическим.
и иметь одинаковые коэффициенты уменьшения (искажения) своего изображения по отношению к оригиналу. Для удобства принято считать этот коэффициент равным единице. Такое аксонометрическое проецирование называют изометрическим. y) -
y) -  ,
, ,
, .
.
 z
z








 A
A 

 A
A









 B
B 

 B B
B B 
 z
z



 O y
O y







 x
x

 z
z

 x
x

 z
z



 A
A 

 x y
x y A
A 




 z
z

 A
A  A
A 





 A
A  x y
x y









 B
B 
 B
B 
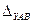 A
A  A
A  D
D 

 D
D  > Z
> Z 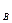 ). А и С – фронтально конкурирующие точки; B и D – профильно конкурирующие точки. Обозначение точки в скобках означает, что её изображение закрыто.
). А и С – фронтально конкурирующие точки; B и D – профильно конкурирующие точки. Обозначение точки в скобках означает, что её изображение закрыто.



 A
A  B
B 


