
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Конструктивные задачи графического моделированияСодержание книги
Поиск на нашем сайте
Конструктивными называют задачи, связанные с конструированием геометрических фигур, их взаимного положения, а так же взаимного положения их элементов по заданным условиям. Эти задачи являются, обычно, разновидностью комплексных, включая в себя, как правило, несколько позиционных и метрических задач. Решение конструктивных задач связано с реализацией на чертеже заданных геометрических условий.При описании геометрических условий и решений конструктивных задач геометрические фигуры (линии и поверхности) удобно моделировать, как множество точек или множество прямых, отвечающих заданным условиям.
Примеры конструктивных задач со множеством точек (ВМТ)
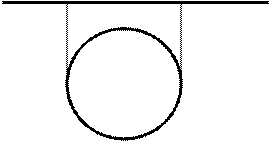
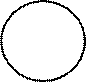
Пример 1 (рис. 8.1). Построить на заданной плоскости Решение Это окружность m на заданной плоскости
Пример 2 (рис. 8.2). Построить ВМТ, равноудалённых от заданной пространственной точки О. Решение Это сфера
Рис. 8.1
O
Рис. 8.2
Пример 3 (рис 8.3). Построить ВМТ, равноудалённых от заданной прямой i.
Решение Это цилиндр вращения
i
Рис. 8.3
Пример 4 (рис. 8.4). Построить ВМТ, равноудалённых от двух заданных точек А и В. Решение Это плоскость
M
A
Рис. 8.4
Пример 5 (рис. 8.5). Построить прямую a, все точки которой были бы равноудалены от заданных точек А и В, при этом прямая a должна быть параллельной плоскости Решение Прямая а расположена в плоскости
A
a
Рис. 8.5
Пример 6 (рис. 8.6). Построить ВМТ, равноудалённых от двух заданных пересекающихся плоскостей: Решение Это две биссекторные плоскости:
Рис. 8.6
Примеры конструктивных задач со множеством прямых линий (ВМП)
Пример 1 (рис.8.7). Построить всё множество прямых (ВМП), проходящих через заданную точку A перпендикулярно заданной прямой b.
Решение Это плоскость
f
f
Рис. 8.7
Пример 2 (рис. 8.8). Даны скрещивающиеся прямые линии: а и b. Построить ВМП, пересекающих прямую a и параллельных прямой b.
Решение Это плоскость
Рис. 8.8
Пример 3 (рис. 8.9). Построить ВМП, равноудалённых от заданной прямой а.
Решение Это цилиндр вращения
Рис. 8.9
Пример 4 (рис. 8.10). Построить ВМП, проходящих через заданную т. А и пересекающих заданную плоскость
Решение Это конус вращения
Рис. 8.10
Пример 5 (рис. 8.11). Построить ВМП, равнонаклонённых к пересекающимся плоскостям
Решение Это биссекторные и перпендикулярные им плоскости
Рис. 8.11
Пример 6. Определить геометрическую фигуру, представляющую собой ВМП, скрещивающихся с заданной прямой i под одинаковым углом и равноотстоящих от неё.
Решение Это однополостный гиперболоид вращения с осью вращения i.
Примеры решения конструктивных задач
Пример 1 (рис. 8.12). Построить ВМТ, равноудалённых от двух заданных параллельных прямых а и b.
Решение Это плоскость
Рис. 8.12
Пример 2 (рис. 8.13). В заданной грани АВС построить ВМТ, равноудалённых от заданных точек М и К, расположенных вне плоскости
Решение
Это прямая m – результат пересечения плоскости
Пример 3 (рис. 8.14). В плоскости
Решение
Всё множество прямых l, которые проходят через точку А под углом
B
m B
Рис. 8.13
h
l
h
Рис. 8.14
Пример 4 (рис. 8.15). Построить ВМП, проходящих через заданную точку М и касательных к заданной сфере
Решение Это конус
Рис. 8.15
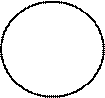
Пример 5 (рис. 8.16). На прямой а определить точки, равноудалённые от заданной точки А на заданном расстоянии r.
Решение Это точки В и С – точки пересечения с прямой а окружности m радиусом r и с центром в точке А, лежащей в плоскости
Рис. 8.16
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 388; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.007 с.) |

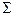 всё множество точек (ВМТ), равноудалённых от заданной на ней точки O.
всё множество точек (ВМТ), равноудалённых от заданной на ней точки O. с центром в т. О.
с центром в т. О.
 O
O  m
m 




 O
O 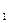 m
m 

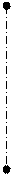

 O
O 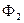






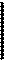











 A
A 
 .
.

 a
a 

 M
M 




 A
A 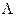 и
и  .
.





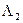


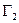
 f), проходящая через заданную точку А перпендикулярно прямой b.
f), проходящая через заданную точку А перпендикулярно прямой b. A
A 



 h
h 


 A
A 


 с
с 


 b
b 

 c
c 
 a
a  b
b 




 A
A 
















 a
a 
 b
b 





 b
b 

 b
b 





 a
a 


 a
a  к плоскости проекций
к плоскости проекций  i
i 
 , являющихся результатом пересечения этого конуса
, являющихся результатом пересечения этого конуса 


 m
m 





 A
A 

 C
C  A
A 
 b
b 




 A
A 
 i
i 






 h
h 



















 A
A  h
h  с вершиной в точке М и касательный к сфере
с вершиной в точке М и касательный к сфере  = i
= i  . Решающее положение: оси i
. Решающее положение: оси i 








 M
M 





 M
M 



 = i
= i 






 .
.





 a
a 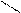
 B
B 







 A
A 


 r
r







