
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
III. Расчет погрешности прямых измерений и доверительного интервала методом, основанным на определении средней квадратичной погрешности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть величина 1. Вычисляют среднее арифметическое значение измеряемой величины:
2. Находят абсолютные погрешности отдельных измерений:
..........
3. Вычисляют квадраты абсолютных погрешностей отдельных измерений:
4. Определяют дисперсию (отклонение случайной величины от её среднего значения) по формуле (если
5. Определяют среднюю квадратичную погрешность результата серии измерений:
6. По заданной доверительной вероятности (надежности) и числу проведенных измерений из таблицы находят соответствующее значение коэффициента Стьюдента 7. Вычисляют абсолютную погрешность всех измерений
8. Сравнивают полученное значение абсолютной погрешности а) если при сравнении окажется, что
б) если окажется, что
Внимание. За абсолютную погрешность простых измерительных приборов (линейки, мензурки, секундомера и т.п.) принимают половину цены наименьшего деления шкалы прибора. Абсолютную погрешность электроизмерительных приборов (и многих других) определяют по классу точности. в) если окажется, что величина абсолютной погрешности результата
где
9. Вычисляют относительную погрешность Е результата измерений:
Пример. При измерении температуры тела в однородных группах обследуемых получена следующая выборка: 1. Находим среднее арифметическое значение температуры (по формуле 27):
2. Находим абсолютную погрешность отдельного измерения:
3. Вычисляем квадраты абсолютных погрешностей отдельных измерений: 4. Вычисляем дисперсию по формуле 30
5. Средняя квадратичная погрешность результата измерения (формула 31) равна: 6. Для доверительной вероятности 7. Абсолютная погрешность
8. Сравниваем полученное значение абсолютной погрешности с абсолютной погрешностью медицинского термометра, которая равна половине цены деления, т.е. ∆tтерм = 9. Пренебрегаем абсолютной погрешностью медицинского термометра и записываем окончательный результат (формула 36): Примечание: Из правил округления в теории погрешностей имеется существенное исключение: при округлении погрешностей последняя цифра увеличивается на единицу, если старшая отбрасываемая цифра 3 или больше трех. В нашем случае 10. Вычисляем относительную погрешность Е (формула 37) результата измерения температуры тела:
IV. Расчет погрешностей косвенных измерений. Пусть определяемая величина N является функцией нескольких переменных x, y, z величин, измеряемых непосредственно (прямые измерения), то есть N=f(x, y, z). Заметим, что в частном случае косвенно измеренная величина может выражаться только через одну прямую измеренную величину (например, объем шара V= 1. Находят среднее арифметическое значение прямых измерений каждой величины x, y, z.
2. Вычисляют среднее арифметическое значение искомой величины: 3. Вычисляют абсолютные погрешности отдельных измерений всех величин 4. Определяют дисперсию каждой измеренной величины:
5. Рассчитывают средние квадратичные погрешности всех величин x, y, z: 6. Вычисляют среднюю квадратичную погрешность искомой величины по формуле:
где частные производные 7. Находят полуширину доверительного интервала искомой величины 8. Окончательный результат записывают в виде:
Доверительную вероятность считать равной Проведем выполнение математической обработки. 1. Найдем средние арифметические значения высоты и диаметра (формула 39): 2. Найдем среднее арифметическое значение объёма цилиндра:
Δ h1= 0,2мм; Δ d1= -0,1мм; Δ h2= -0,4мм; Δ d2= 0,2мм; Δ h3= 0; Δ d3= -0,3мм; Δ h4= 0,2мм; Δ d4= 0; Δ h5= -0,2мм; Δ d5= 0,1мм. 4. Вычисляем дисперсию высоты Dh и диаметра Dd (формула 41):
5. Вычисляем средние квадратичные погрешности высоты
6. Рассчитываем среднюю квадратичную погрешность объёма цилиндра V (формула 43):
7. По таблице для α=0,95 и n =5находим значение коэффициента Стьюдента: 8. Вычисляем полуширину доверительного интервала ΔV: ΔV= 9. Записываем окончательный результат в виде: V= 10. Относительная погрешность:
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.162.33 (0.007 с.) |

 непосредственно измерена n раз, при этом получены результаты
непосредственно измерена n раз, при этом получены результаты  . Результаты каждого измерения заносят в таблицу. Явно ошибочные результаты (промахи) отбрасывают.
. Результаты каждого измерения заносят в таблицу. Явно ошибочные результаты (промахи) отбрасывают. (если n<30) (27)
(если n<30) (27)  (если n>30) (28)
(если n>30) (28)

 (29)
(29)
 ):
): (30)
(30) (31)
(31) .
. и, следовательно, границы доверительного интервала (полуширину доверительного интервала):
и, следовательно, границы доверительного интервала (полуширину доверительного интервала): (32)
(32) :
: , то за абсолютную погрешность результата берется абсолютная погрешность прибора
, то за абсолютную погрешность результата берется абсолютная погрешность прибора  ;
; 
 гораздо больше
гораздо больше  (34)
(34) (35),
(35), - значение коэффициента Стьюдента, соответствующее выбранной надежности
- значение коэффициента Стьюдента, соответствующее выбранной надежности  и бесконечно большому числу измерений (
и бесконечно большому числу измерений ( ). На практике значение коэффициента Стьюдента
). На практике значение коэффициента Стьюдента  берут из таблицы при
берут из таблицы при  . Окончательный результат записывают в форме:
. Окончательный результат записывают в форме: (36).
(36). (37)
(37) . Сделать интервальную оценку среднего значения температуры при доверительной вероятности 0,95.
. Сделать интервальную оценку среднего значения температуры при доверительной вероятности 0,95.




 при
при  коэффициент Стьюдента (из таблицы) равен:
коэффициент Стьюдента (из таблицы) равен:  .
. результата измерений (полуширина доверительного интервала – формула 32) равна:
результата измерений (полуширина доверительного интервала – формула 32) равна: .
.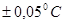 . Следовательно
. Следовательно 
 .
. .
. .
. (38), где d – диаметр шара).
(38), где d – диаметр шара).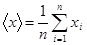 ;
;  ;
;  (39).
(39). (40).
(40).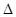 xi,
xi,  ;
;  ;
;  (41).
(41).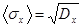 ;
;  ;
;  (42).
(42).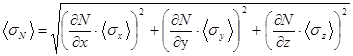 (43),
(43), рассчитывают при
рассчитывают при  ,
,  ,
,  . При получении выражения для любой частной производной остальные аргументы функции
. При получении выражения для любой частной производной остальные аргументы функции  считают постоянными.
считают постоянными. , определив из таблицы значение коэффициента Стьюдента для заданной вероятности
, определив из таблицы значение коэффициента Стьюдента для заданной вероятности  и данного числа измерений (для всех измеряемых величин необходимо задавать одно и то же значение доверительной вероятности):
и данного числа измерений (для всех измеряемых величин необходимо задавать одно и то же значение доверительной вероятности): 
 (44).
(44).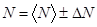 (45).
(45). ).
). (46).
(46). ;
;  .
. ;
; 
 ;
; ;
; и диаметра
и диаметра  :
: 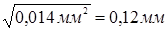 ;
; .
. ;
;  ;
;  ;
; ;
; 
 .
.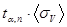 ; ΔV=2,8·5,5мм3 =15,4 мм3.
; ΔV=2,8·5,5мм3 =15,4 мм3. V; V=(233,7
V; V=(233,7  15,4) мм3.
15,4) мм3. .
.


