Модели биологических мембран

Уточнение строения биомембран и изучение их свойств осуществляется с использованием физико-химических моделей мембраны.

Первая модель – монослой. Молекулы фосфолипидов, будучи помещенными на границу раздела вода-воздух (вода-масло), выстраиваются в один слой так, что гидрофильные (полярные) головки погружаются в воду, а гидрофобные «хвосты» в контакт с водой не вступают, остаются в воздухе (масле). Молекулы фосфолипидов как бы «отслаиваются» от воды. Пока молекул немного, они располагаются на поверхности «прильнув» к воде головками и выставив наружу «хвосты» (рис. 3)

Рис. 3

Если постепенно уменьшать площадь, занимаемую монослоем, удастся получить монослой, в котором молекулы расположены так же плотно, как и в одном из монослоев мембраны. При изменении состояния липидных молекул (под действием температуры, взаимодействия липидов с различными лекарственными препаратами и пр.) меняется площадь, занимаемая молекулами.

Поэтому в билогических и медицинских исследованиях широко используются монослои синтетических липидов, изолированных на различных природных мембранах.

Вторая модель – плоские бислойные липидные мембраны (БЛМ).

 

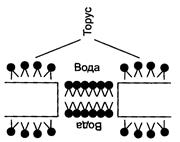
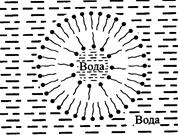
Рис.4

Такие мембраны получают на маленьких отверстиях диаметром около 1 мм в пластинке из пластика (например, фторопласта), погруженной в водную среду. На отверстие наносят каплю раствора липида (в спирте, хлороформе, гептане и других растворителях). Растворитель диффундирует из раствора в воду и на отверстии остается пленка липида. Эта пленка спонтанно утончается до тех пор, пока не образуется бимолекулярный слой толщиной около 6 нм. Лишний липид собирается в виде ободка-торуса у краев отверстия (рис. 4).На плоских мембранах можно проводить электрические измерения. Эта система особенно полезна для изучения пор, каналов или переносчиков, которые облегчают или ускоряют перенос заряда через бислой из одного водного компартамента в другой. В водные камеры нетрудно поместить электроды, растворы в них можно легко заменять, а измерение тока и напряжение высокоточных и высокочувствительных.

Третья модель – липосома. Липидные слои, если они имеют большую протяженность, стремятся замкнуться сами на себя, чтобы спрятать гидрофобные «хвосты» от воды. При этом образуются фосфолипидные везикулы – липосомы (рис. 5).

Рис. 5.

Они представляют собой мельчайшие пузырьки (везикулы), состоящие из билипидной мембраны. Липосомы фактически являются биологической мембраной, полностью лишенной белковых молекул. На липосомах часто проводят эксперименты по изучению влияния различных факторов на свойства мембраны, или, наоборот, влияния мембранного окружения на свойства встраиваемых белков. В медицине липосомы используются для доставки лекарственных веществ, приготавливая их в среде, содержащей чужое вещество, в определенные органы и ткани. Таким способом готовят липосомные кремы и мази в дерматологии и косметологии. Сами липосомы не токсичны, полностью усваиваются в организме и являются надежной липидной микрокапсулой для направленной доставки лекарства.

 

5. Перенос молекул (атомов) через мембраны, уравнение Фика.

Явления переноса – это самопроизвольные необратимые процессы, в которых благодаря молекулярному движению из одной части системы в другую переносится какая-либо физическая величина.

К явлениям переноса относятся:

- диффузия (перенос массы);

- вязкость (перенос импульса из слоя в слой);

- теплопроводность (перенос энергии);

- электропроводность (перенос электрического заряда).

Как синоним переноса частиц в биофизике используется термин транспорт частиц.

Диффузия – явление самопроизвольного переноса массы вещества из области с большей концентрацией в область с меньшей. Диффузия приводит к равномерному распределению вещества по всему объему. Количественно диффузия описывается специальными параметрами.

1. Потоком вещества ( Ф ) через элемент поверхности, который перпендикулярен направлению диффузии, называется количество этого вещества, переносимого через данный элемент за единицу времени.

Ф = - D ^.(dc/dх)^.S, где

D – коэффициент диффузии. Знак (-) означает, что поток направлен в сторону убывания концентрации вещества.

2. Плотностью потока вещества (I) называется отношение потока вещества (Ф) через элемент поверхности к площади этого элемента (S):

I =Ф/S

Подставив в эту формулу выражение для потока уравнением диффузии (уравнением Фика):

I = - D dc/dх

Знак (-) показывает, что суммарная плотность потока вещества при диффузии направлена в сторону, противоположную градиенту концентрации.

Рассмотрим в качестве примера поток незаряженных частиц через биологическую мембрану.

Обратим внимание на следующий известный факт: на границе раздела двух сред (например, воды и масла) обязательно имеет место скачкообразное изменение концентрации частиц диффундирующего вещества.

Коэффициент распределения вещества (к) – это величина, равная отношению концентраций частиц в граничащих средах:

К = с_{1 среда} / с_{2 среда}

Вещество, диффундирующее через мембрану, преодолевает три барьера (рис.6)

Рис. 6

а) примембранный слой,

б) саму мембрану,

в) противоположный примембранный слой.

Коэффициент распределения вещества между мембраной и окружающей средой равен коэффициенту распределения вещества между мембраной и клеткой:

к = с_нар^м/ с_нар = с _вн^м/ с_вн

Поэтому с_нар^м = к с_нар, с _вн^м = к с_вн.

Причем, величины с_нар и с_вн. можно измерить.

Учитывая малую толщину мембраны, можно считать, что концентрация молекул диффундирующего вещества изменяется в ней линейно. Поэтому градиент концентрации диффундирующего вещества постоянен:

dc/dх = (с_нар^м - с _вн^м)/L

Запишем выражение для плотности потока:

I = -D (с_нар^м - с _вн^м)/L,

или учитывая коэффициент распределения вещества, получим

I = Dк (с _вн - с_нар)/L.

Введем коэффициент проницаемости мембраны (Р)

Р = Dк/L,

который зависит от коэффициента диффузии, а также от толщины мембраны и коэффициента распределения вещества между мембраной и окружающей средой. Под проницаемостью понимают способность мембраны пропускать сквозь себя определенные вещества.

Окончательно получаем уравнение Фика для диффузии в мембранах:

I = Р(с_вн - с_нар)

6. Перенос заряженных частиц, электродиффузионное уравнение Нернста – Планка.

Рассмотрим перенос ионов. При отсутствии внешнего воздействия между поверхностями мембраны существует разность потенциалов, то есть в мембране постоянно есть электрическое поле. При отсутствии градиента концентрации главная движущая сила при переносе ионов – это электрическое поле.

На отдельный ион в электрическом поле действует сила

f₀= qE, где

Е – напряженность электрического поля, в котором находится ион, а

q = ze – заряд иона (z – валентность иона).

Если учесть, что Е = - grad φ = - dφ /dx, можно записать:

f₀= ze (dφ /dx).

На один моль ионов будет действовать сила

f = f₀N_a. = - z e N_a (dφ /dx) = - zN_a F (dφ /dx), где

N_a – постоянная Авогадро, F = e N_a - постоянная Фарадея.

Помимо электрической силы, на ионы действуют так же силы сопротивления. Поэтому движение ионов является равномерным и характеризуется средней скоростью v. Между средней скоростью движения ионов и силой, действующей на один моль, существует прямо пропорциональная зависимость:

v= u_мf, где

u_м – коэффициент пропорциональности, называемый подвижностью ионов.

Запишем

v = - u_м z F (dφ /dx),

Чтобы найти поток вещества, переносимый ионами через элемент

поверхности S, выделим цилиндрический объем электролита, ограниченный двумя такими элементами. Длину цилиндра l выразим через скорость и время:

l =vt. Объем цилиндра: V = Sl = Svt

За время t все ионы, находящиеся в цилиндре, пройдут через левую площадку S. Количество перенесенного при этом вещества равно произведению концентрации на объем: m = cV = cSvt (кг) или ν = cSvt (моль).

Найдем поток вещества Ф: Ф = cSv

Плотность потока: I = Ф/S = сv.

Используя, что v = - ν_м z F (dφ /dx), получим I = -cν_м z F (dφ /dx).

В общем случае перенос частиц определяется как градиентом их концентрации, так и воздействием электрического поля:

I = - D dc/dx - cν_м z F dφ /dx.

Это - уравнение Нернста-Планка (электродиффузионное уравнение). Оно устанавливает зависимость плотности диффузионного потока от концентрации ионов и от напряженности электрического поля.