
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
VII. Упрощенный метод обработки результатов прямых измерений с использованием средней абсолютной погрешности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть проведено
1. Находим среднее арифметическое значение
2. Вычисляем абсолютные погрешности результатов отдельных измерений
..........
Знак «+»(или «-») у абсолютной погрешности данного значения означает, что результат этого измерения получился больше (или меньше) среднего значения измеряемой величины. 3. Вычисляем среднюю абсолютную погрешность всего опыта, как среднее арифметическое абсолютных значений (модулей) абсолютных погрешностей отдельных измерений.
4. Сравнивают полученное значение средней абсолютной погрешности Если окажется, что Такая замена вызвана тем, что с помощью данного измерительного прибора принципиально нельзя измерить величину с большей точностью, чем точность самого прибора, определяемая его собственной погрешностью. 5. Вычисляют относительную погрешность результата серии измерений:
Данный метод не даёт точных результатов и поэтому в научных исследованиях, как правило, не используется. Его можно применять для расчета погрешностей в условиях учебного процесса, когда проведено не более 5 измерений, т.е. это облегченный вариант математической обработки результатов малого количества измерений. Пример. При измерении сопротивления резистора омметром было сделано 5 измерений, результаты которых занесены в таблицу:
1. Вычисляем среднее арифметическое сопротивление резистора (промахи отсутствуют):
2. Вычисляем абсолютные погрешности результатов отдельных измерений: ΔR1=3,00 Ом - 3,00 Ом=0,00 Ом ΔR2=3,00 Ом - 2,99 Ом=0,01 Ом ΔR3=3,00 Ом - 3,00 Ом=0,00 Ом ΔR4=3,00 Ом - 3,01 Ом=-0,01 Ом ΔR5=3,00 Ом - 3,00 Ом=0,00 Ом 3. Находим среднюю абсолютную погрешность серии измерения сопротивления резистора:
4. Сравним полученное значение средней абсолютной погрешности измерения сопротивления с абсолютной погрешностью используемого омметра. Класс точности омметра 0,1. Верхний предел шкалы 5 Ом. Абсолютная погрешность омметра равна Так как 5. Записываем конечный результат измерения сопротивления резистора:
6. Относительная погрешность равна:
Задачи для самостоятельного решения. 1. В университет было подано 1300 заявлений от девушек и 980 заявлений от юношей. Найти относительные частоты подачи заявлений для этих абитуриентов. 2. Найти вероятность выпадения нечётного числа при бросании игральной кости. 3. С помощью микроскопа измеряли диаметр эритроцитов человека. При этом были получены следующие значения: 5мкм, 8мкм, 11мкм, 6мкм. Найти доверительный интервал размера эритроцита с доверительной вероятностью 0,95. 4. Милливольтметром на 400 В (номинальное значение шкалы) измерены напряжения в 50мВ, 200мВ, 300мВ. Определить абсолютную и относительную погрешности для каждого случая, если класс точности прибора 1,0. Дополнительными погрешностями пренебречь. 5. Почему рекомендуется подбирать электроизмерительные приборы с известным классом точности так, чтобы измеряемая величина составляла 70-90% от величины, на которую рассчитана вся шкала прибора? 6. Пример решения задачи: Задача: В урне находится 8 шаров: 5 белых и 3 чёрных. Из неё наугад извлекают один шар. Какова вероятность P(A) того, что этот шар белый? Вероятность P(B), что этот шар чёрный? Решение. Анализируем условие задачи. В урне находятся одинаковые шары, которые отличаются друг от друга только цветом. При извлечении шаров наугад появление каждого из них следует считать равновозможными событиями. Пусть m – число благоприятствующих событий, n – число всех возможных независимых событий при однократном испытании. Запишем условие и решение задачи в символической форме.
 Опр. Р(А) и Р(Б) Опр. Р(А) и Р(Б)
1) белого шара 2) чёрного шара: Ответ: вероятность появления белого шара 0,625, вероятность появления чёрного шара 0,375. Тесты для самоконтроля. Уровень.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.83.210 (0.009 с.) |

 измерений величины
измерений величины  и получено
и получено  . Полученные результаты необходимо свести в таблицу. Промахи отбрасывают.
. Полученные результаты необходимо свести в таблицу. Промахи отбрасывают.

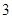




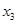

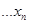
 измеряемой величины:
измеряемой величины: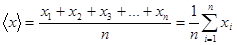
 , как разности между средним значением измеряемой величины и значением, полученным при данном измерении:
, как разности между средним значением измеряемой величины и значением, полученным при данном измерении:

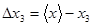


 с абсолютной погрешностью измерительного прибора
с абсолютной погрешностью измерительного прибора  . Если при сравнении окажется, что
. Если при сравнении окажется, что  , то конечный результат записывают в виде:
, то конечный результат записывают в виде: 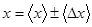 .
. .
. или
или 
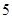






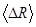 меньше
меньше  , то за абсолютную погрешность измерения принимаем абсолютную погрешность омметра
, то за абсолютную погрешность измерения принимаем абсолютную погрешность омметра  .
.
 . Тогда вероятность извлечения:
Для белого шара:
. Тогда вероятность извлечения:
Для белого шара: 

 Р(А) =5/8=0,625
Р(А) =5/8=0,625 Р(Б) =3/8=0,375
Р(Б) =3/8=0,375


