
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы обработки опытных данныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ГОУ ВПО «ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» МЕДИЦИНСКИЙ ИНСТИТУТ КАФЕДРА ФИЗИКИ И ГУМАНИТАРНЫХ ДИСЦИПЛИН
Тищенко А.А., Митяев В.В., Шманева О.Н.
СЕМИНАРЫ ПО ФИЗИКЕ Учебное пособие для самостоятельной работы студентов медицинского института
Орел 2009 УДК 53(075.8) Т479 Печатается по решению редакционно-издательского Совета Орловского государственного университета, протокол № 2 от 2 сентября 2008 года.
Семинары по физике Учебное пособие для самостоятельной работы студентов медицинского института
Авторы: Тищенко А.А. – зав. кафедрой физики и гуманитарных дисциплин МИ ОГУ, кандидат педагогических наук, профессор кафедрой физики и гуманитарных дисциплин МИ ОГУ; Митяев В.В. – кандидат технических наук, профессор кафедры теоретической физики и математического моделирования ОГУ; Шманева О.Н. - старший преподаватель кафедры физики и гуманитарных дисциплин МИ ОГУ.
Под редакцией зав. кафедрой физики и гуманитарных дисциплин МИ ОГУ Тищенко А.А.
Рецензенты: Золотарев Ю.В. – директор МИ ОГУ, доктор медицинских наук, профессор; Байдак Г.В. – кандидат химических наук, профессор кафедры общей физики ОГУ.
Пособие содержит материал к 5 семинарам по физике для студентов 1 курса Медицинского института ОГУ специальностей «лечебное дело» и «педиатрия». В учебном пособии для каждого семинара даны: основные вопросы, рассматриваемые на семинаре; определения основных понятий; краткое содержание теории по данному вопросу; образцы решения задач; трехуровневые тесты самоконтроля; список литературы. В пособии содержится объем информации, который должен быть усвоен будущим врачом для лучшего понимания процессов, происходящих в организме, для ознакомления с основами физических методов диагностики и лечения.
© Авторы, 2009 © ГОУ ВПО Орловский государственный университет, 2009 ОГЛАВЛЕНИЕ Введение…………………………………………………………………....4
1.Семинар №1. Статистические методы обработки опытных данных…...5
2.Семинар №2.Механические колебания и волны………………………..38
3. Семинар №3.Акустика, Звук. Ультразвук и инфразвук……………… 52
4. Семинар №4. Биоэнергетика и термодинамика биологических систем……………………………………………………………………….74
5. Семинар №5. Биофизика клетки. Физические механизмы переноса через биологические мембраны……………………………………………91
6. Семинар №6.Рентгеновское излучение. Радиоактивность. Дозиметрия…………………………………………………………..……..114
7. Литература...……………………………………………………………...119
ВВЕДЕНИЕ. Семинар (seminarium – в переводе с латинского «рассадник знаний») – один из основных методов обсуждения учебного материала в высшей школе. Семинары проводятся по наиболее важным и сложным разделам изучаемого курса физики. Они проводятся с целью углубленного изучения дисциплины, привития обучающимся навыков самостоятельного поиска и анализа информации, формирования и развития научного мышления, умения активно участвовать в творческих дискуссиях, аргументировано отстаивать свое мнение. Основные задачи семинара состоят в том, чтобы: - углубить и закрепить знания, полученные на лекциях и в ходе самостоятельной работы; - привить обучающимся навыки поиска, обобщения и изложения учебного материала; - выработать умение формировать, обосновывать и излагать собственные суждения по изучаемому материалу, отстаивать свое мнение. Данное учебное пособие призвано облегчить начинающему обучаться в ВУЗе в поиске необходимой информации при подготовке к семинарским занятиям. Готовясь к семинару, студент должен: -заранее по плану семинара уяснить тему, цель и рассматриваемые вопросы; - определить свою роль и задачу на семинаре (написание реферата, подготовка выступления с докладом, в прениях по обсуждаемым вопросам и т.д.); - ознакомиться с рекомендованной литературой; - глубоко изучить рассматриваемые на семинаре вопросы; - подготовить конспект своего выступления, реферата; - решить задачи, ответить на вопросы тестовых заданий. В учебном пособии к каждому семинару указывается тема, цель, список рекомендуемой литературы, список рассматриваемых вопросов, краткое их содержание, задачи для самостоятельного решения и примеры решения задач, тестовые задания двух уровней. Полный список рекомендуемой литературы приведен в конце пособия. В начале каждого семинара указывается в зашифрованном виде необходимый список литературы. Первая цифра – это номер источника в списке литературы. Дальнейшие слова, цифры означают главу, лекцию или номера страниц. Например: «7.- Главы 1-3» означает «7. Ремизов А.Н., Максина А.Г., Потапенко А.Я. Медицинская и биологическая физика.- М.: Дрофа, 2004, главы 1,2,3»
СЕМИНАР №1 Мотивация цели В медицине, биологии приходиться иметь дело с различными показателями, полученными в результате измерений, которые характеризуют состояние биологической системы (температура тела больного, артериальное давление, дозировка лекарств и т.д.). В результате несовершенства измерительной аппаратуры, непостоянства условий измерений, погрешностей методов измерений, несовершенства наших органов чувств и других причин все измерения физических величин можно выполнить только с известной степенью точности. Поэтому важно знать, как получены те или иные величины, какова степень приближения результатов измерений к истинному значению, в каких единицах они представлены, знать основные методы учёта ошибок измерений и уметь применять на практике. Очевидно, что достоверность будет тем большей, чем меньше отклонение (погрешность) результатов от истинного значения измеряемой величины. Следовательно, неотъемлемой частью любого эксперимента является оценка точности измерения различных физических величин. Вопросами оценки результатов измерений с заданной степенью надежности занимается специальный раздел теории вероятности математическая статистика -раздел математики, посвященный методам регистрации, обработки, систематизации и использования экспериментальных данных для научных и практических выводов. Цель занятия: изучить статистические методы обработки опытных данных, подчиняющихся нормальному закону распределения случайных величин; научиться вычислять полуширину доверительного интервала для заданной надежности (доверительной вероятности) прямых и косвенных измерений. Подготовка к семинарскому занятию Изучить по рекомендованной литературе и данному пособию следующие вопросы: I. Измерения физических величин и возникающие при этом погрешности (ошибки). Абсолютная и относительная погрешности. II. Некоторые понятия теории вероятностей и математической статистики. 1. Понятие случайного события. Достоверные, невозможные, несовместимые и равновозможные события. Относительная частота появления события. 2. Вероятность случайного события. Классическое и статистическое определение вероятности. 3. Дискретные случайные величины и их числовые параметры: математическое ожидание, дисперсия, среднее квадратичное отклонение. III. Законы распределения непрерывной случайной величины и формы их задания: 1. Распределение Максвелла; 2. Распределение Больцмана; 3. Нормальный закон распределения Гаусса; 4. Доверительный интервал, доверительная вероятность (надёжность); 5.Зависимость доверительного интервала от надёжности, числа измерений и коэффициента Стьюдента. IV.Алгоритм обработки результатов косвенных измерений. V. Точность измерительных приборов: 1) класс точности; 2) нахождение абсолютной и относительной погрешностей измерительных приборов. VI. Графический метод представления результатов измерения. Теоретические сведения I. Основные понятия и формулы. Теория вероятностей – раздел математики, в котором выясняются закономерности, возникшие при взаимодействии большого числа факторов или событий. Событие – это всякий результат или исход опыта. Случайное событие – это событие, которое может при осуществлении данных условий как произойти, так и не произойти и для которого имеется определённая вероятность его появления. Относительная частота события P*(А) в серии опытов определяется отношением числа m появлений этого события к общему числу n проведённых измерений: P*(А) Вероятность – числовая характеристика, степень возможности появления какого-либо случайного события при тех или иных условиях. Статическая вероятность события (закон больших чисел) это предел, к которому стремится частота события при неограниченном увеличении числа испытаний: P (A) = Несовместимые события – это события, которые не могут произойти одновременно. Событие невозможно, если P(A) = 0. Событие достоверное, если P(A) = 1, т.е. в результате эксперимента оно должно произойти обязательно. Дискретная случайная величина – это случайная величина, принимающая только определённые числовые значения. Условие нормировки для дискретной случайной величины, имеющей n значений:
Непрерывная величина – величина, принимающая любые значения в данном интервале. Простой статистический ряд – совокупность всех значений случайной величины, записанных в порядке их получения. Выборка (выборочная совокупность) – часть значений (x Математическое ожидание Для эмпирических распределений статистическим аналогомматематического ожидания является среднее арифметическое значение Математическим ожиданиемнепрерывной случайной величины X служит интервал: M (X) = где f(x) – плотность вероятности (функция распределения вероятностей). Дисперсия D(Х) дискретной случайной величины X характеризует отклонение (рассеяние) этой случайной величины от её среднего значения (математического ожидания) и для опытных данных определяется формулой: D(Х) = Среднее квадратичное отклонение < < Закон распределения случайной величины – это совокупность всех возможных значений X Нормальный закон распределения случайных величин (закон Гаусса).
где <x> - математическое ожидание (среднее значение) случайной величины <x> = M (X);
f (x) – плотность вероятности (функция распределения вероятностей). Распределение Больцмана: n = n где n – концентрация молекул воздуха, находящихся в гравитационном поле Земли на высоте h; n Т – температура; m – масса молекулы; к – постоянная Больцмана; g – ускорение свободного падения. Закон распределения молекул в газах по скоростям называется распределением Максвелла.
где mо – масса молекулы, k – постоянная Больцмана, Т – абсолютная температура газа, Гистограмма (от греч. histos – столб, gramma – черта, столбчатая диаграмма)- один из способов графического изображения статистических распределений какой-либо величины; представляет собой совокупность смежных прямоугольников, построенных на одной прямой. Доверительный интервал – интервал, в который с определенной (доверительной) вероятностью попадает истинное значение измеряемой или исследуемой величины. Доверительной вероятностью (надёжностью) результата серии измерений называется вероятность того, что истинное (действительное) значение измеряемой величины попадает в данный доверительный интервал. Среднее арифметическое значение n измерений величины X: <X> = Абсолютная погрешность отдельного измерения:
Средняя абсолютная погрешность опыта для измерений: < Относительная погрешность опыта: Е =
II. Основы теории ошибок и методы её практического применения для обработки экспериментальных данных Все физические явления и свойства характеризуются различными физическими величинами. Для науки и техники большое значения имеют количественные характеристики, полученные в процессе измерения. Измерить физическую величину - это значит найти опытным путём её значение с помощью специальных технических средства. В результате измерения данная физическая величина сравнивается с её значением (эталоном), условно принятым за единицу. Все измерения делятся на прямые (или непосредственные) и косвенные. Прямым измерением называется такое измерение, при котором значение измеряемой величины получают путем непосредственного сравнения с её мерой или с помощью соответствующего прибора. Этим способом измеряют сравнительно небольшое число физических величин (измерение длины линейкой, время - секундомером, напряжение - вольтметром, температуру - термометром и др.). Косвенным измерением называется такое измерение, при котором значение искомой величины рассчитывают по формуле с помощью известной зависимости между искомой величиной и величинами, определяемыми путем прямых измерений. Например, определение объема тела по прямым измерениям его геометрических размеров, определение удельного сопротивления цилиндрического проводника прямыми измерениями длины, диаметра поперечного сечения и электрического сопротивления проводника и др. Различают истинное и действительное значение физической величины. Под истинным значением физической величины понимают ее значение, которое абсолютно верно отражало бы эту величину. Проводя измерения физической величины, мы никогда не можем получить абсолютно точно истинное ее значение. Действительным значением физической величины называется ее значение, найденное экспериментальным путем и настолько близкое к истинному значению, что для поставленной измерительной задачи может его заменить. Действительным значением измеряемой величины считают ее значение, полученное с помощью образцового прибора. При измерении физических величин под действием самых разнообразных причин возникают погрешности измерений, т.е. отклонения результатов измерений от действительных значений искомых величин. Погрешности, допускаемые при измерениях, принято делить на три типа: систематические, случайные и промахи (грубые ошибки). Систематической погрешностью называют такую погрешность, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины одним и тем же методом и с помощью одних и тех же измерительных приборов. Систематические погрешности появляются вследствие неисправности приборов (например, отклонение стрелки вольтметра или амперметра от нулевого деления при отсутствии тока), неточности метода исследований, каких - либо упущений экспериментатора, использование для вычислений неточных формул и т.д. Систематические погрешности можно обнаружить только при внимательном и критическом отношении к состоянию и работе измерительных приборов, условиям измерения и получаемым результатам. Таким образом, систематические погрешности могут быть устранены или учтены. Случайной погрешностью называется погрешность, которая обусловлена действием не поддающихся контролю многочисленных факторов, влияние которых невозможно учесть. Такие погрешности отличаются друг от друга в отдельных измерениях и носят случайную непредсказуемую величину. Методы определения случайных погрешностей рассматриваются в теории погрешностей, основанной на математической статистике и теории вероятностей, позволяющей по данным измерений вычислить наиболее вероятное значение измеряемой величины и оценить погрешность измерений. Промах (грубая ошибка) - это такая погрешность измерения, которая оказывается значительно больше ожидаемых при данных условиях. Промах может возникнуть при небрежном выполнении измерений, неверно записанных показаний приборов, явном несоблюдении условий эксплуатации приборов и т.д. Промах можно интуитивно обнаружить, сравнивая числовые значения полученных результатов или их абсолютных погрешностей. Промахи должны быть исключены из результатов измерений. Решение. Анализируем условие задачи. В урне находятся одинаковые шары, которые отличаются друг от друга только цветом. При извлечении шаров наугад появление каждого из них следует считать равновозможными событиями. Пусть m – число благоприятствующих событий, n – число всех возможных независимых событий при однократном испытании. Запишем условие и решение задачи в символической форме.
 Опр. Р(А) и Р(Б) Опр. Р(А) и Р(Б)
1) белого шара 2) чёрного шара: Ответ: вероятность появления белого шара 0,625, вероятность появления чёрного шара 0,375. Тесты для самоконтроля. Уровень. Тесты 2-го уровня. Дополните. 1. Систематической погрешностью называют такую погрешность, которая 1)……. 2)…….. или 3)…….. 4)…….. при повторных измерениях одной и той же величины одним и тем же методом и с помощью одних и тех же измерительных приборов.
2. Величины, которые в зависимости от обстоятельств могут принимать 1)……. значения, называются 2)………. 3. Для величин, подчиняющихся нормальному закону распределения, 1)…… 2)……. значением измеряемой величины является ее 3)…… 4)…… значение.
4.Совокупность всех значений случайной величины называется 1)……. 2)…….. рядом.
5. Расчетами показано, что вероятность попадания нормально распределенной случайной величины в интервале значений от <x>–s до <x>+s в среднем равна 1)……%, а в интервале (<x>–3s;<x>+3s) – уже 2)………%..
УСТАНОВИТЕ СООТВЕТСТВИЯ:
6.
Ответ: 1…..; 2…….; 3…….
7.Укажите, каким величинам соответствуют формулы, позволяющие обсчитывать результаты прямых измерений.
8.
Ответ: 1……; 2……; 3…..; 4……
9. Ответ: 1…..; 2…..; 3…..; 4……; 5…..; 6…..; 7…… 9. Укажите, каким вопросам соответствуют формулы, позволяющие обсчитывать результаты косвенных измерений для функции х = у· z
СЕМИНАР № 2 ВОПРОСЫ ДЛЯ САМОПОДГОТОВКИ. 1. Гармонические колебания (смещение, амплитуда, фаза, скорость и ускорение колеблющейся точки). 2. Уравнение динамики гармонического колебательного движения. 3. Кинетическая и потенциальная энергия колебательного движения. 4. Затухающие колебания: А) уравнение динамики свободных затухающих колебаний; Б) уравнение кинематики свободных затухающих колебаний; В) декремент затухания; Г) логарифмический декремент затухания. 5. Вынужденные колебания, Автоколебания. Резонанс. А) уравнение динамики вынужденных колебаний; Б) уравнение кинематики вынужденных колебаний; В) резонанс; Г) автоколебания. 6. Механические волны. А) уравнение плоской волны; Б) поток энергии и интенсивность волны; В) линейная и групповая скорости волны. 7. Эффект Доплера.
Мотивация цели. Повторяющиеся движения или изменения состояния называют колебаниями. Всем колебаниям, в независимости от природы, присущи общие закономерности. Колебания распространяются в средах в виде волн. В живом организме, а так же при диагностике и лечении заболеваний широко распространены процессы с повторением различных состояний и описывающих их параметров. Лучше понять распространение упругих колебаний и волн в сосудах, работу сердца, легких, восприятие звука, распространение биопотенциалов и свойства других колебательных процессов поможет знание основных параметров и закономерностей колебательных движений. Самыми простыми для изучения и понимания являются механические колебания. Цель занятия изучить основные понятия, законы и закономерности простейших механических колебаний и волн; применять основные положения теории колебаний и волн к процессам, протекающим в организме, а также при диагностике и лечении заболеваний. Подготовка к практическому занятию. Изучить по рекомендованной литературе, уметь объяснять и пояснять примерами следующие вопросы: I. Основные понятия. Колебания и волны. Свободные колебания. Параметры колебательных движений: смещение, амплитуда, фаза, циклическая частота, и др. II. Основные законы теории колебаний и волн. 1.Уметь выводить уравнения динамики и кинематики свободных гармонических незатухающих и затухающих колебаний, а так же вынужденных колебаний. Знать основные параметры колебательного и волнового движения. 2. Энергия колеблющейся точки. Энергия волны. Поток энергии. Интенсивность волны. 3. Автоколебательные процессы. 4. Явления резонанса. 5. Эффект Доплера.
Теоретические сведения. I. Основные понятия. Колебания - периодически повторяющиеся процессы или явления. Смещение – отклонение колеблющейся точки от положения равновесия. Амплитуда – максимальное отклонение колеблющейся точки от положения равновесия или максимальное смещение. Фаза колебаний – параметр, однозначно определяющий положение колеблющейся точки в пространстве. Условно фаза это угол поворота радиус-вектора Циклическая частота – угловая скорость вращения радиус-вектора Период – время одного полного колебания, время цикла. Частота – число полных колебаний за единицу времени. Скорость – первая производная смещения по времени ν=dх/dt. Ускорение – первая производная скорости по времени α=dν/dt или вторая производная смещения по времени α=d2х/dt2. Квазиупругая сил а – сила, действие которой аналогично действию силы упругости, определяемой законом Гука (F=-kx). Математический маятник – материальная точка массой m, подвешенная на тонкой невесомой нити длиной ℓ. Пружинный маятник - материальная точка массой m, прикрепленная к невесомой пружине жесткостью k. Физический маятник – протяженное тело различной формы и размеров, совершающее колебания около точки подвеса или опоры.. Свободные колебания – колебания, происходящие в системе за счет однократного сообщения ей энергии. Гармонические колебания – колебания, происходящие по закону sin или cos. (х=Аcos(ωt+φ0)) Затухающие колебания – колебания с уменьшающейся амплитудой. Вынужденные колебания – колебания под действием внешнего изменяющегося фактора (силы). Резонанс – явление достижения максимальной амплитуды вынужденных колебаний при заданных ω0 – циклической частоты собственных колебаний и β – коэффициента затухания. Декремент затухания – отношение двух последовательных амплитуд, разделенных интервалом времени, равном периоду колебаний ( Логарифмический декремент затухания – натуральный логарифм отношения двух последовательных амплитуд, разделенных интервалом времени, равном периоду колебаний. Логарифмический декремент затухания - натуральный логарифм декремента затухания. ( Автоколебания – незатухающие колебания, существующие в системе с затуханием при отсутствии переменного внешнего воздействия. Механическая волна – механическое возмущение, распространяющееся в среде и несущее энергию. Фронт волны – поверхность, в которой все точки волны колеблются в одинаковой фазе. Плоская волна – волна, фронт которой является плоским. Фазовая скорость – скорость распространения фиксированной фазы колебаний. Групповая скорость – скорость группы синусоидальных волн. Поток энергии – средняя энергия, переносимая волной в единицу времени ( Интенсивность – поток энергии через единичную площадь, расположенную перпендикулярно направлению распространения волны ( Эффект Доплера – изменение частоты волн, воспринимаемых приемником (наблюдателем), вследствие относительного движения источника и приемника волн. ( II. Основные законы теории колебаний и волн. 1. Гармонические колебания. Гармонические колебания – колебания, происходящие по гармоническому закону (закону синуса или косинуса). Х = А sin (ωt + φ0). (1) В уравнении 1: А - амплитуда колебаний; (ωt + φ0) – фаза колебаний; φ0- начальная фаза; ω – круговая (циклическая) частота.
вектора Рассмотрим колебания горизонтального пружинного маятника. Один

Запишем это уравнение в проекции на ось Х: ma=Fу или m(d2x/dt2)= -kx Разделим обе части уравнения на m и перенесем все слагаемые в левую часть уравнения (d2x/dt2 )+ (k/m)x=0. Введем обозначения (k/m)=ω02, где ω0 - циклическая частота собственных колебаний. Перепишем уравнение (d2x/dt2 ) + ω02 x=0 (2) Получили уравнение второго порядка гармонических колебаний, так как решением его является уравнение гармонических колебаний Х=Аcos(ω0t + φ0) Если подставить в уравнение 2 значения d2x/dt2 (d2x/dt2 =-А ω02 cos(ω0t + φ0)) и X (Х=Аcos(ω0t + φ0)), то получим -А ω02 cos(ω0t+φ0) +А ω02 cos(ω0t+φ0)=0. Следовательно Х=Аcos(ω0t + φ0) является решением уравнения 2. Круговая частота ω связана с частотой колебаний υ соотношением υ= ω/2π. Период колебаний Т=1/υ =2π/ω. Для пружинного маятника Т=2π Скорость материальной точки колеблющейся по гармоническому закону: ν = dx/dt= - Aωsin(ωt + φ0) (3); ν = - νmax sin(ωt + φ0)= νmax cos((ωt + φ0)+π/2), где νmax= Aω. Фаза скорости больше фазы смещения на π/2. Ускорение а = dν/dx =- Aω2 cos(ωt + φ0) (3); a = - amax cos(ωt + φ0) =amax cos((ωt + φ0) + π) (4), где amax = Aω2. Ускорение и смещение находятся в противофазе. Кинетическая энергия колеблющейся материальной точки Ек = (½)mν2 =(½)m A 2ω 2sin 2(ωt + φ0) Ек =(½)k A 2sin 2(ωt + φ0) (5), где mω 2=k. Потенциальная энергия Еп =(½)к х2 =(½)к А 2cos 2(ωt + φ0) (5) Полная механическая энергия Е= Ек+ Еп=(½)k A 2 (sin 2(ωt + φ0)+ cos 2(ωt + φ0)) =(½)k A 2 (6) При отсутствии сил трения полная механическая энергия сохраняется. Затухающие колебания. Действие сил трения существенно изменяет характер движения, колебание становится затухающим. Рассмотрим колебания горизонтального пружинного маятника.
На тело действуют сила тяжести
Запишем это уравнение в проекции на ось Х: ma=Fу+Fтр или m(d2x/dt2)= -kx – r(dx/dt). Разделим обе части уравнения на m и перенесем все слагаемые в левую часть уравнения (d2x/dt2 )+ (r/m) (dx/dt) +(k/m)x=0. Введем обозначения (r/m)=2β и (k/m)=ω02, где β - коэффициент затухания, а ω0 - циклическая частота собственных колебаний. Перепишем уравнение (d2x/dt2 )+ 2β(dx/dt) + ω02 x = 0 (7) Получили уравнение второго порядка затухающих колебаний. Решение этого уравнения существенно зависит от знака разности ω2= ω02 – β2, где ω циклическая частота затухающих колебаний. При ω02 – β2>O решение записывается в следующем виде: X=A0e-βt cos(ωt +φ0) (8), где (A0e-βt) - амплитуда затухающих колебаний, которая изменяется по экспоненциальному закону. Период затухающих колебаний Т=2π/ω= При очень малом трении (ω02 >> β2) Т=2π/ω0. Быстрота убывания амплитуды колебаний определяется коэффициентом затухания β: чем больше β, тем сильнее торможение. На практике степень затухания характеризуют логарифмическим декрементом затухания λ =ℓn | |||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 (1)
(1)
 ; при этом
; при этом  (2)
(2) .
. , x
, x  ,…x
,…x  ) случайной величины, отобранных для исследования из общей совокупности всех её значений.
) случайной величины, отобранных для исследования из общей совокупности всех её значений. дискретной случайной величины X есть сумма произведений всех её возможных значений x
дискретной случайной величины X есть сумма произведений всех её возможных значений x  на их вероятности P
на их вероятности P  (3)
(3) .
. (4),
(4),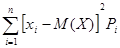 (5)
(5) > - корень квадратный из дисперсии:
> - корень квадратный из дисперсии: =
=  (6)
(6) (7),
(7), - среднее квадратичное отклонение;
- среднее квадратичное отклонение; - основание натурального логарифма (неперово число);
- основание натурального логарифма (неперово число); exp (-mgh/кТ) (8),
exp (-mgh/кТ) (8), (9),
(9), - скорость молекулы.
- скорость молекулы. =
= 
 (10)
(10) =
=  (i = 1,2,…n)
(i = 1,2,…n) X> =
X> =  =
=  (11)
(11)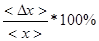 (12)
(12) . Тогда вероятность извлечения:
Для белого шара:
. Тогда вероятность извлечения:
Для белого шара: 

 Р(А) =5/8=0,625
Р(А) =5/8=0,625 Р(Б) =3/8=0,375
Р(Б) =3/8=0,375 е) x=<x>±ta nσ
е) x=<x>±ta nσ

 в) <x>=<y>< z>
г) ∆x=ta nσх
д)
в) <x>=<y>< z>
г) ∆x=ta nσх
д) 
 е) х = <x>±∆x
и) абвгде
к) авдбге
л) егвабд
е) х = <x>±∆x
и) абвгде
к) авдбге
л) егвабд
 (амплитуды).
(амплитуды). ).
). ).
). ).
). ).
). ).
).

 (1)
(1)
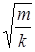 , для математического T =2π
, для математического T =2π  , для физического маятника
, для физического маятника  (I - момент инерции тела относительно оси, m –масса маятника, h – расстояние между центром тяжести и осью вращения).
(I - момент инерции тела относительно оси, m –масса маятника, h – расстояние между центром тяжести и осью вращения).
 сила упругости пружины
сила упругости пружины  , сила трения
, сила трения  , нормальная реакция опоры
, нормальная реакция опоры  . Запишем 2-й закон Ньютона.
. Запишем 2-й закон Ньютона. =
=  +
+  +
+  .
. .
.


