Комплексный чертеж окружности

 

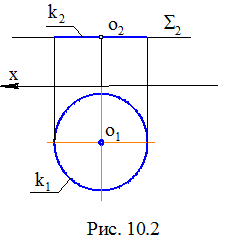
Если окружность расположена в плоскости уровня, то на одну плоскость проекций она проецируется в отрезок, а на другую – в окружность (в натуральную величину). На рис.10.2 показан комплексный чертеж окружности k, расположенной в горизонтальной плоскости уровня S. На P₂ окружность проецируется в отрезок (часть прямой S₂), а на P₁ – в окружность.

Окружность, расположенная в плоскости, не параллельной и не перпендикулярной плоскости проекций, проецируется на эту плоскость в кривую, которая называется эллипсом. Диаметры окружности будут проецироваться в отрезки, которые называются диаметрами эллипса. Длина диаметра эллипса равна длине диаметра окружности, умноженной на косинус угла наклона диаметра окружности к плоскости проекций. Диаметр окружности, расположенный на линии уровня, проецируется в натуральную величину, так как угол наклона его к плоскости проекций равен нулю. Этот диаметр будет больше всех остальных диаметров, он и назван большим диаметром эллипса. Диаметр окружности, перпендикулярный большому, наклонен к той же плоскости проекций под наибольшим углом. Его называют малым диаметром эллипса.

Построение эллипса по большому и малому диаметрам, которые взаимно перпендикулярны, приведено ниже. На рис. 10.3 показано построение одной точки эллипса. Так, пусть даны: AB – большой диаметр эллипса; CD – малый диаметр эллипса. После проведения большой окружности диаметром AB и малой окружности диаметром CD, проводим произвольный луч m. Через точку 1 на большой окружности проводим отрезок, параллельный малой оси CD, а через точку 2 на малой окружности – отрезок, параллельный большой оси AB. Точка пересечения построенных отрезков является точкой эллипса (точка M). Проводя множество лучей, проходящих через точку O (проекция центра окружности), и повторяя показанные построения, получим множество точек эллипса. Затем по лекалу, соединяя эти точки, получим эллипс.

На рис 10.4 показана последовательность построения эллипса по большому диаметру и точке эллипса. Даны: AB – большой диаметр эллипса; M – точка эллипса. Последовательность построений показана стрелками. Эти построения следуют из рассмотренных на рис. 10.3. После определения точки 2, а значит, и малой оси CD, можем перейти к построению любого числа точек эллипса, как показано на рис. 10.3.

 

 

 

 

Пусть окружность радиуса R расположена теперь во фронтально проецирующей плоскости D, центр окружности – точка O. Для нахождения большого диаметра эллипса необходима линия уровня. Через точку O проведем горизонталь h (h₁, h₂) в плоскости D. На h₁ отложим отрезки O₁A₁=O₁B₁, длины которых равны R. Отрезок A₁B₁ – это большой диаметр эллипса, в который проецируется окружность на П₁. Через точку O в плоскости D проведем фронталь f(f₁,f₂). На f₂ отложим отрезки O₂C₂=O₂D₂, длины которых равны R. Точки C и D являются точками окружности, которые расположены на фронтали f. Горизонтальные проекции этих точек принадлежат f₁ (точки C₁ и D₁). Так как отрезок C₁D₁ перпендикулярен большому диаметру A₁B₁, то C₁D₁ – это малый диаметр эллипса на П₁. Теперь по большому диаметру A₁B₁ и малому диаметру C₁D₁ строим эллипс (горизонтальная проекция окружности). Фронтальной проекцией окружности является отрезок C₂D₂, так как D – фронтально проецирующая плоскость и все фронтальные проекции точек окружности расположены на прямой D₂ между точками C₂ и D₂. То же самое получим, если будем строить эллипс на П₂ по большому диаметру C₂D₂ и малому диаметру, величина которого равна нулю.

Если окружность расположена в плоскости общего положения, то она проецируется на П₁ в эллипс (горизонтальная проекция окружности) и на П₂ – тоже в эллипс (фронтальная проекция окружности). В этом случае эллипсы строятся по большому диаметру и точке. Пусть плоскость общего положения, в которой расположена окружность радиуса R, задана прямыми h (h₁, h₂) и f (f₁,f₂). Обратим внимание на то, что в качестве прямых, задающих плоскость, взяты ее главные линии – горизонталь и фронталь. Точка O – центр окружности. На h₁ строим большой диаметр 1₁2₁ (|O₁1₁|=|O₁2₁|=R). Это большой диаметр горизонтальной проекции окружности. На f₂ строим большой диаметр 3₂4₂ (|O₂3₂| = |O₂4₂| = R). Это большой диаметр фронтальной проекции окружности. Строим для точки 3 горизонтальную проекцию 3₁. На П₁ имеем 1₁2₁ – большой диаметр эллипса, 3₁ – точка эллипса. Строим для точки 2 фронтальную проекцию 2₂. На П₂ имеем 3₂4₂ – большой диаметр эллипса, 2₂ – точка эллипса. Теперь каждую из проекций окружности можно построить по большому диаметру и точке. Если при задании плоскости окружности горизонталь и фронталь не использовались, то их нужно провести, а затем выполнить описанные выше построения.