
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 3. Кривые второго порядка. ОкружностьСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1. Найти уравнение окружности, центр которой находится в точке (3;-5) и радиус которой равен 4. 3.2. Найти уравнение окружности радиуса 2 с центром в точке (-4/5;3/5). 3.3. Найти точки пересечения оси Ox с окружностью, диаметром которой служит отрезок, соединяющий точки (1;2) и (-3;-4). 3.4. Найти уравнение окружности, диаметром которой является отрезок прямой 3x-4y+12=0, содержащийся между осями координат. 3.5. Найти уравнение окружности, диаметром которой является общая хорда окружностей: 3.6. Найти уравнение окружности радиуса а, касающейся оси Oy в начале координат. 3.7. Найти центр и радиус окружности 3.8. Найти центр и радиус окружности 3.9. Найти уравнение прямой, проходящей через центр окружности 3.10. Найти уравнение окружности, проходящей через точки (0;2), (2;0) и (0;0). 3.11. Найти уравнение окружности, описанной около треугольника, вершинами которого являются точки (0;1), (-2;0) и (0;-1). 3.12. Найти уравнение окружности, описанной около равнобедренного треугольника, высота которого равна 5 единицам длины и основанием которого служит отрезок, заключенный между точками (-4;0), (4;0). 3.13. Найти уравнение окружности, описанной около треугольника, сторонами которого являются прямые x+2y-3=0, 3x-y-2=0, 2x-3y-6=0. 3.14. Найти уравнение окружности, касающейся осей координат и проходящей через точку (4;-2). 3.15. Центр окружности, касающейся осей координат, лежит на прямой 3x-5y+15=0. Найти уравнение окружности. 3.16. Окружность, радиус которой равен 5 единицам длины, проходит через точки (4;-2) и (5;-3). Найти уравнение этой окружности. 3.17. Центр окружности, которая проходит через точки (-2;4) и (-1;3), лежит на прямой 2x-3y+2=0. Найти уравнение этой окружности. Тема 4. Эллипс 4.1. Найти длины осей, эксцентриситет и координаты фокусов эллипса 4.2. Найти длины осей, эксцентриситет и координаты фокусов эллипса 4.3. Найти координаты вершин и фокусов и эксцентриситет эллипса 4.4. Определить, при каких значениях a и b эллипс 4.5. Найти уравнение эллипса, две вершины которого имеют координаты ( 4.6. Две вершины эллипса имеют координаты ( 4.7. Найти уравнение эллипса, фокусы которого имеют координаты 4.8. Найти уравнение эллипса, координаты фокусов которого (0; 4.9. Найти уравнение эллипса, у которого длина малой оси равна 6 и один из фокусов имеет координаты (-4;0). 4.10. Найти уравнение эллипса, если известно, что он проходит через точки 4.11. Найти уравнение эллипса, если известно, что он проходит через точки 4.12. Большая ось эллипса лежит на оси Оx и длина ее равна 6; эксцентриситет эллипса равен ½. Найти уравнение эллипса. 4.13. Эксцентриситет эллипса равен 1/3, ордината точки эллипса, абсцисса которой равна абсциссе фокуса, равна 4 единицам длины. Найти уравнение эллипса. 4.14. Найти уравнение эллипса, у которого эксцентриситет равен 1/3 и абсцисса одного из фокусов равна 3/2. 4.15. Найти эксцентриситет эллипса, если известно, что длина ординаты точки его, абсцисса которой равна абсциссе фокуса, равна 2/3 длины малой полуоси. 4.16. Найти точки пересечения эллипса Тема 5. Гипербола 5.1. Найти эксцентриситет, координаты фокусов и уравнения асимптот гиперболы 5.2. Найти эксцентриситет, координаты фокусов и уравнения асимптот гиперболы 5.3. Найти эксцентриситет, координаты фокусов и уравнения асимптот гиперболы 5.4. Найти уравнение гиперболы, у которой фокусы имеют координаты 5.5. Найти уравнение гиперболы, асимптотами которой являются прямые 5.6. Найти уравнение гиперболы, асимптотами которой являются прямые 5.7. Найти уравнение равносторонней гиперболы, проходящей через точку (3;-1). 5.8. Найти уравнение гиперболы, если известно, что она проходит через точки 5.9. Найти точки пересечения гиперболы а) 2x + 3y = 0; б) 4x – 3y = 0; в)20x + 21y +12=0; г) 2x – y – 3 =0. 5.10. Найти точки пересечения равнобочной гиперболы 5.11. Найти уравнение гиперболы, координаты фокусов которой 5.12. Две вершины эллипса расположены в фокусах гиперболы, вершины которой лежат в фокусах эллипса. Уравнение эллипса есть Тема 6. Парабола 6.1. Составить уравнение параболы, если известно, что: а) осью симметрии параболы служит ось Оx, вершина лежит в начале координат и расстояние от вершины до фокуса равно 6 единицам длины; б) парабола симметрична относительно оси Оx, проходит через точку (2;-5) и вершина ее лежит в начале координат; в) парабола симметрична относительно оси Оx, фокус лежит в точке (0;4) и вершина – в начале координат. г) парабола симметрична относительно оси Оx, проходит через точку (-2;4) и вершина ее лежит в начале координат; д) парабола симметрична относительно оси Оy, проходит через точку (6;3) и вершина ее лежит в начале координат; е) парабола симметрична относительно оси Оy, проходит через точку (-6;-3) и вершина лежит в начале координат. 6.2. Парабола проходит через точку (-1;-1) и имеет вершину в точке (-3/2;2). Найти уравнение параболы, если ось ее параллельна оси Оy. 6.3. Вершина параболы лежит в точке (2;3); парабола проходит через начало координат, и ось ее параллельна оси Оx. Найти уравнение параболы. 6.4. Найти координаты вершины и фокуса, уравнения оси и директрисы параболы 6.5. Найти координаты вершины и фокуса, уравнения оси и директрисы параболы 6.6. Найти уравнение параболы, если начало координат совпадает с фокусом и осью параболы служит ось Оx; параметр равен р. 6.7. Найти уравнение параболы, если ось кривой и директриса приняты соответственно за оси Оx и Оy; параметр равен р. 6.8. Найти уравнение параболы, вершина которой находится в точке (3;2) и фокус в точке (5;2). 6.9. Найти уравнение параболы, вершина которой лежит в точке (-1;-2) и фокус в точке (-1;-4). 6.10. Найти уравнение параболы, у которой фокус лежит в точке (2;-1), а директрисой служит прямая y-4=0. 6.11. Найти уравнение параболы, у которой вершина лежит в точке (-2;-5), а директрисой является прямая x-3=0 6.12. Найти уравнение параболы, у которой вершина лежит в точке (5;-2), а директрисой является прямая y+4=0. 6.13. Найти координаты вершины и фокуса, уравнения оси и директрисы параболы:
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 681; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.5 (0.008 с.) |

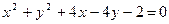 и
и  .
. .
. .
. и перпендикулярной прямой x-2y+1=0.
и перпендикулярной прямой x-2y+1=0. .
. .
. .
. проходит через точки (2;3), (-1;-4).
проходит через точки (2;3), (-1;-4). ), а один из фокусов – координаты (2;0).
), а один из фокусов – координаты (2;0). ; координаты фокусов
; координаты фокусов  Найти уравнение эллипса.
Найти уравнение эллипса. , а длина большой оси равна 10.
, а длина большой оси равна 10. и длина большой оси равна 12.
и длина большой оси равна 12.


 с прямыми а) y=4x; б) x=6; в) 2x-y-9=0; г) x-y+8=0.
с прямыми а) y=4x; б) x=6; в) 2x-y-9=0; г) x-y+8=0. .
. .
. .
. и действительная ось равна 6.
и действительная ось равна 6. и фокусы которой имеют координаты
и фокусы которой имеют координаты 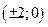 .
. и проходящей через точку (2;1).
и проходящей через точку (2;1). .
. с прямыми:
с прямыми: с окружностью
с окружностью 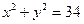 .
. и действительная ось равна 4.
и действительная ось равна 4.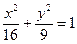 . Найти уравнение гиперболы.
. Найти уравнение гиперболы. .
. .
.



