Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раздел III. Математический анализСодержание книги
Поиск на нашем сайте
Тема 11. Функция Найти области определения функций:
Исследовать на четность и нечетность функции:
Построить графики функций:
11.26. Дана функция 11.27. Даны функции f(x)= 11.28. Даны функции 11.29. Даны функции Тема 12. Непрерывность. Предел 12.1. Найти приращение функции 12.2. Найти приращение функции y=1/x в точке 12.3. Доказать непрерывность функции 12.4. Доказать непрерывность функции 12.5. Найти область определения функции Вычислить пределы вида
Вычислить пределы вида
Вычислить пределы с неопределенностью вида
Вычислить пределы, используя первый замечательный предел:
Вычислить пределы, используя второй замечательный предел:
Исследовать на непрерывность функции, найти точки разрыва и указать характер разрыва:
Тема 13. Производная 13.1. Найти приращение функции y=2x-1 в точке x=2, при: а) 13.2. Вычислить приращение функции в точке x, если приращение аргумента равно 13.3. Составить отношение 13.4. Используя определение, найти производные функций: Найти производные функций по формулам дифференцирования:
Найти производные второго порядка функций:
Найти производные функций, заданных параметрически:
13.51. Показать, что функция удовлетворяет уравнению:
13.52. Показать, что функция
13.53. Найти угловой коэффициент касательной к параболе 13.54. Найти угловой коэффициент касательной к гиперболе 13.55. В какой точке касательная к параболе 13.56. Доказать, что касательная к гиперболе Тема14. Приложение производной Вычислить пределы, используя правило Лопиталя (предварительно убедившись в возможности его применения):
Найти интервалы монотонности и экстремумы функции:
Найти наибольшее и наименьшее значение (глобальный максимум и минимум) функции y=f(x) на отрезке [a,b]: 14.25. 14.27. f(x)=x ln x на [0,1;1]. 14.28. 14.29. Найти наибольшее и наименьшее значение функции y=f(x) на интервале (a;b): 14.31. 14.33. 14.35. Найти стороны прямоугольника наибольшей площади, вписанного в круг радиуса r. 14.36. Бак цилиндрической формы должен вместить V литров воды. Каковы должны быть его размеры, чтобы поверхность (без крышки) была наименьшей? 14.37. Требуется выделить прямоугольную площадку земли в 512 14.38. Окно имеет форму прямоугольника, завершенного полукругом. При заданном периметре окна найти такие его размеры, чтобы оно пропускало наибольшее количество света.
Найти точки перегиба и интервалы выпуклости и вогнутости графиков функций:
Найти асимптоты графиков функций:
Исследовать функции и построить их графики:
Тема 15. Дифференциал Найти дифференциалы следующих функций:
Найти дифференциалы второго порядка функций:
Пользуясь понятием дифференциала вычислить приближенно:
|
||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 514; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.223.185 (0.01 с.) |


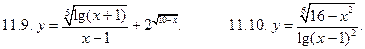
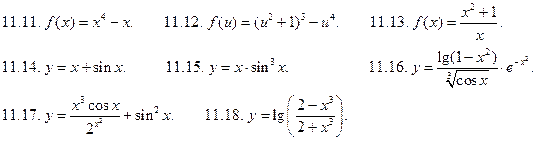


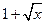 и
и  . Составить функции f(x)+g(x), f(x).g(x), f(x)/g(x) и найти их области определения.
. Составить функции f(x)+g(x), f(x).g(x), f(x)/g(x) и найти их области определения.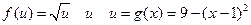 . Составить сложную функцию y=
. Составить сложную функцию y=  и найти ее область определения.
и найти ее область определения. . Составить сложную функцию y=f(x) и найти ее область определения.
. Составить сложную функцию y=f(x) и найти ее область определения.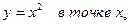 , соответствующее приращению аргумента
, соответствующее приращению аргумента 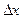 .
.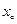 , соответствующее приращению аргумента
, соответствующее приращению аргумента 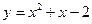 в любой точке ее области определения.
в любой точке ее области определения.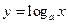 в любой точке ее области определения.
в любой точке ее области определения.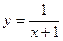 и доказать непрерывность этой функции в любой точке ее области определения.
и доказать непрерывность этой функции в любой точке ее области определения.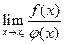 с неопределенностью вида
с неопределенностью вида 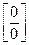 . (В этом случае необходимо разложить на множители и числитель и знаменатель дроби, или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.)
. (В этом случае необходимо разложить на множители и числитель и знаменатель дроби, или домножить и числитель, и знаменатель дроби на одно и то же выражение, приводящее к формулам сокращенного умножения. Неопределенность устраняется после сокращения дроби.)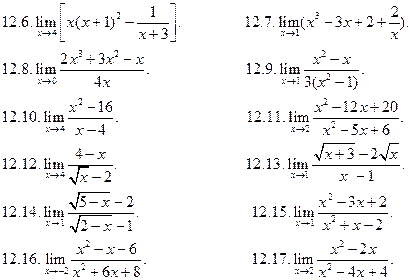
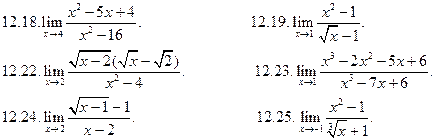
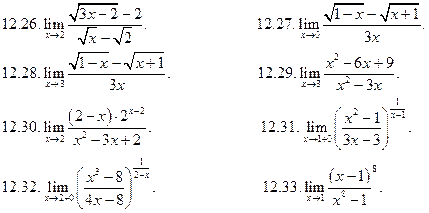
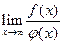 с неопределенностью вида
с неопределенностью вида 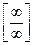 , где f(x) и
, где f(x) и 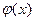 в общем случае – сложные степенные или показательные функции. (В случае степенных функций необходимо выносить за скобку в числителе и знаменателе x с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.)
в общем случае – сложные степенные или показательные функции. (В случае степенных функций необходимо выносить за скобку в числителе и знаменателе x с наибольшим показателем степени среди всех слагаемых дроби; в случае показательных функций за скобку выносится наиболее быстро возрастающее слагаемое среди всех слагаемых дроби. После сокращения дроби неопределенность устраняется.)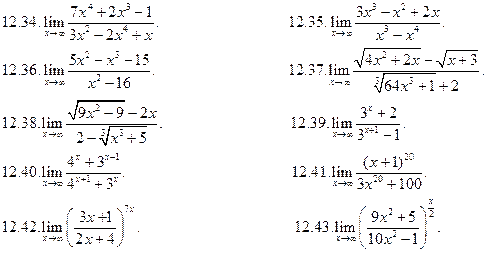

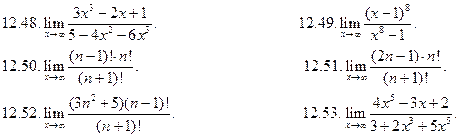
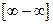 . (Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2-му типу после приведения дробей к общему знаменателю. Если упомянутая функция представляет собой алгебраическую сумму иррациональных выражений, то неопределенность или устраняется, или приводится к предыдущему типу пределов путем домножения и деления функции на одно и то же (сопряженное) выражение, приводящее к формулам сокращенного умножения).
. (Если функция, стоящая под знаком предела, представляет собой алгебраическую сумму дробей, то неопределенность устраняется или приводится ко 2-му типу после приведения дробей к общему знаменателю. Если упомянутая функция представляет собой алгебраическую сумму иррациональных выражений, то неопределенность или устраняется, или приводится к предыдущему типу пределов путем домножения и деления функции на одно и то же (сопряженное) выражение, приводящее к формулам сокращенного умножения).
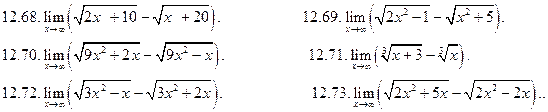


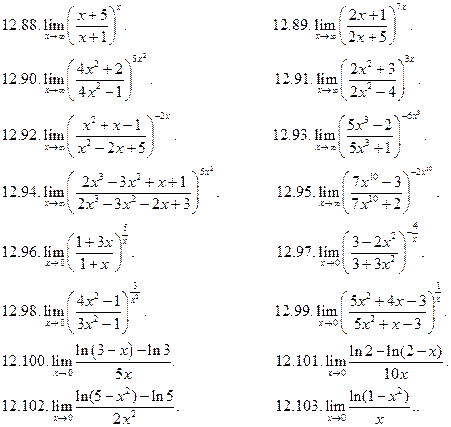


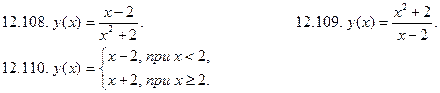

 :
: 
 для функций:
для функций: 



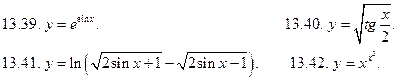


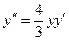 .
. удовлетворяет уравнению:
удовлетворяет уравнению: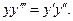
 : а) в точке (0;0); б) в точке (2;4); в) в точках пересечения параболы с прямой y=-x+6.
: а) в точке (0;0); б) в точке (2;4); в) в точках пересечения параболы с прямой y=-x+6. в точках: а) (0;-1); б) (2;1).
в точках: а) (0;-1); б) (2;1).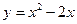 : а) параллельна оси Оx; б) образует с осью Оx угол
: а) параллельна оси Оx; б) образует с осью Оx угол  ?
? не может быть параллельна оси Оx.
не может быть параллельна оси Оx.

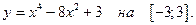 14.26.
14.26. 
 на [0;3].
на [0;3]. на [-1;1]. 14.30.
на [-1;1]. 14.30.  на [-2;0].
на [-2;0]. . 14.32.
. 14.32. 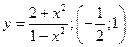 .
. . 14.34.
. 14.34.  .
. , огородить ее забором и разделить загородкой на три равные части параллельно одной из сторон площадки. Каковы должны быть размеры площадки, чтобы на постройку заборов пошло наименьшее количество материала?
, огородить ее забором и разделить загородкой на три равные части параллельно одной из сторон площадки. Каковы должны быть размеры площадки, чтобы на постройку заборов пошло наименьшее количество материала?