
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возрастание и убывание функции. Экстремумы функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Функция Функция Функция Если функция Если функция Если в любой точке Рассмотрим функцию Точка Точки максимума и минимума функции называются точками экстремума функции. Значения функции в точках экстремума называются экстремумами функции. Если функция Если функция
1) 2) 3) Если в критической точке 1) если 2) если Примеры с решениями Пример 1. Найти интервалы возрастания и убывания функции Решение. Область определения функции Можно поступить и так: находим точки, в которых
Интервалы, на которых производная функции имеет знак «+», являются интервалами возрастания функции, а те, на которых «−» − интервалами убывания. Ответ: функция возрастает на интервале Пример 2. Найти интервалы монотонности функции Решение. Область определения функции
Изображаем область определения функции и наносим на нее точку
Теперь видим, что на интервале Ответ: функция возрастает на интервале Пример 3. Найти экстремумы функции Решение. Область определения функции Изображаем область определения функции (это вся числовая прямая) и наносим на нее критические точки, после чего определяем знак производной на каждом из образовавшихся интервалов:
По знаку производной на каждом интервале определяем характер монотонности функции и видим точки экстремума. Остается вычислить сами экстремумы функции:
Ответ: Пример 4. Найти экстремумы функции Решение.
Критические точки:
Ответ: Примеры для самостоятельного решения Найти интервалы возрастания и убывания функций:
11.1. 11.2. 11.3. 11.4. 11.5. 11.6. 11.7. 11.8 11.9. 11.10 11.11. 11.12. 11.13. 11.14. Найти экстремумы функций: 11.15. 11.16. 11.17. 11.18. 11.19. 11.20. 11.21.
Ответы 11.1. убывает при 11.2. возрастает при 11.3. убывает при 11.4. возрастает при 11.5. возрастает при 11.6. убывает при 11.7. убывает при 11.8. возрастает при 11.9. возрастает при 11.10. убывает при 11.11. возрастает при 11.12. убывает при 11.13. возрастает при 11.14. убывает при 11.15. 11.16. 11.17. 11.18. 11.19. 11.20. 11.21.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.91.173 (0.007 с.) |

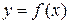 называется возрастающей (убывающей) на интервале
называется возрастающей (убывающей) на интервале  , если она определена на этом интервале (
, если она определена на этом интервале (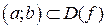 ) и если для любых двух точек
) и если для любых двух точек  и
и  , принадлежащих этому интервалу, из условия
, принадлежащих этому интервалу, из условия  следует неравенство
следует неравенство  (
( ).
).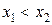 следует неравенство
следует неравенство  (
(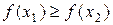 ).
). (
( ) для любого
) для любого  из этого промежутка. При этом точки, в которых
из этого промежутка. При этом точки, в которых  не заполняют никакого отрезка (необходимое условие возрастания (убывания) дифференцируемой функции в промежутке).
не заполняют никакого отрезка (необходимое условие возрастания (убывания) дифференцируемой функции в промежутке). (
( ) для любого
) для любого 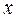 из этого промежутка – необходимое условие неубывания (невозрастания) дифференцируемой функции в промежутке.
из этого промежутка – необходимое условие неубывания (невозрастания) дифференцируемой функции в промежутке. (
( ), то в этом промежутке функция
), то в этом промежутке функция  . Точка
. Точка  из этой окрестности
из этой окрестности  . Значение функции в точке максимума называется максимумом функции:
. Значение функции в точке максимума называется максимумом функции:  .
. называется точкой минимума функции
называется точкой минимума функции 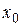 , что для всех
, что для всех  из этой окрестности
из этой окрестности  . Значение функции в точке минимума называется минимумом функции:
. Значение функции в точке минимума называется минимумом функции: 
 или
или  не существует – необходимое условие экстремума. Отсюда следует, что точки экстремума функции следует искать только среди тех точек, в которых производная функции равна нулю или не существует, такие точки называются критическими или стационарными точками функции.
не существует – необходимое условие экстремума. Отсюда следует, что точки экстремума функции следует искать только среди тех точек, в которых производная функции равна нулю или не существует, такие точки называются критическими или стационарными точками функции. меняет знак с «+» на «−», то
меняет знак с «+» на «−», то  , то
, то  , то
, то  .
. . Находим производную
. Находим производную  . Для нахождения интервалов возрастания функции решаем неравенство
. Для нахождения интервалов возрастания функции решаем неравенство  ,
,  , получаем
, получаем  , на этих интервалах функция возрастает. Для нахождения интервалов убывания решаем неравенство
, на этих интервалах функция возрастает. Для нахождения интервалов убывания решаем неравенство 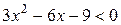 ,
,  , получаем
, получаем  , на этом интервале функция убывает.
, на этом интервале функция убывает. ,
,  ,
,  ,
,  . Эти точки отметим на числовой прямой и определим знаки производной на образовавшихся интервалах:
. Эти точки отметим на числовой прямой и определим знаки производной на образовавшихся интервалах:
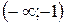 и
и  ; функция убывает на интервале
; функция убывает на интервале 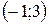

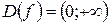 . Находим производную
. Находим производную  , решаем уравнение
, решаем уравнение 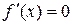 ,
, .
. , после чего определяем знак производной на каждом из образовавшихся интервалов:
, после чего определяем знак производной на каждом из образовавшихся интервалов:
 функция убывает, а на интервале
функция убывает, а на интервале 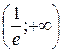 возрастает.
возрастает.
 . Находим производную
. Находим производную  . Находим критические точки:
. Находим критические точки:  не существует при
не существует при  ,
,  при
при  .
.
 .
. .
.

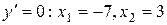





 ,
,  .
.

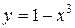

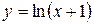



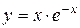

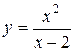










 возрастает при
возрастает при  ;
; и
и  убывает при
убывает при 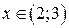 ;
; ;
; и
и  , убывает при
, убывает при  и
и  ;
; ;
; , возрастает при
, возрастает при  ;
;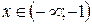 и при
и при  , убывает при
, убывает при  ;
; , убывает при
, убывает при  и при
и при  , возрастает при
, возрастает при  ;
; и при
и при 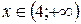 , убывает при
, убывает при  ;
; возрастает при
возрастает при 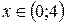 ;
;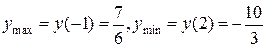 ;
; ;
; ;
; ;
; ;
; ;
;



