
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная функции одной переменной
(определение, геометрический смысл) Рассмотрим функцию Определение 1. Производной функции
Для обозначения производной используют символы: Определение 2. Односторонние пределы
Примеры с решениями Пример 1. Найти Решение. Пусть
Воспользуемся определением производной:
Ответ: Пример 2. Найти Решение. Пусть
Воспользуемся определением:
Ответ: Заметим, что функция С геометрической точки зрения значение производной функции
Уравнение касательной, проведенной к графику функции
Уравнение нормали к графику той же функции в точке с абсциссой x 0:
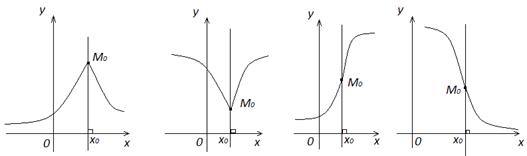
если Если в точке x 0 функция
Уравнение касательной в этих случаях имеет вид: x = x 0, а уравнение нормали – Углом между кривыми
если Если же Пример 3. Составить уравнения касательной и нормали к графику функции Решение. Воспользуемся уравнениями касательной (2) и нормали (3). В эти уравнения надо поставить x 0 = 2;
Ответ:
Пример 4. Пользуясь определением, найти значение производной функции Решение. Выведем формулу производной функции
Итак,
Ответ: Если при прямолинейном движении точки задан закон движения
Примеры для самостоятельного решения 3.1. Вычислить приращение функции 3.2. Вычислить приращение функции 3.3. Найти приращение функции 3.4. Найти приращение функции 3.5. Пользуясь определением производной, вычислить 3.6. Пользуясь определением производной, вычислить 3.7. Пользуясь определением производной, вывести формулу производной функции 3.8. Пользуясь определением производной, вывести формулу производной функции производной в точках:
3.9. Найти угловой коэффициент касательной к графику функции 3.10. Составить уравнения касательной и нормали к графику функции 3.11. На графике функции 3.12. На графике функции 3.13. Составить уравнения касательных к графику функции
3.14. Закон движения точки: Ответы 3.1. 3.5. – 4; 3.6. – 4; 3.7.
3.9.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 935; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.193.172 (0.03 с.) |
 , определенную в точке x и в некоторой окрестности этой точки.
, определенную в точке x и в некоторой окрестности этой точки. (1)
(1)
 называются соответственно левой производной и правой производной функции
называются соответственно левой производной и правой производной функции 
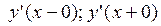 . Для существования производной функции
. Для существования производной функции 
 для функции
для функции  пользуясь определением производной.
пользуясь определением производной. – приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:
– приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:




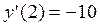
 для функции
для функции  в точке х = 0.
в точке х = 0.
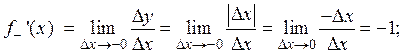

 .
. не имеет производной в точке x= 0, так как
не имеет производной в точке x= 0, так как 
 , где
, где  – угол наклона касательной к оси Оx.
– угол наклона касательной к оси Оx.
 . (2)
. (2)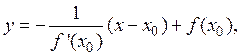 (3)
(3) .
. или
или  или
или  , то касательная к графику этой функции в точке с абсциссой x 0 перпендикулярна оси
, то касательная к графику этой функции в точке с абсциссой x 0 перпендикулярна оси 
 . Если же
. Если же  , то уравнение нормали: x = x 0.
, то уравнение нормали: x = x 0. и
и  называется угол между касательными, проведёнными к этим кривым в точке их пересечения
называется угол между касательными, проведёнными к этим кривым в точке их пересечения 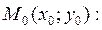
 (4)
(4) .
. , то касательные перпендикулярны и
, то касательные перпендикулярны и  .
. в точке с абсциссой x 0 = 2.
в точке с абсциссой x 0 = 2. и найденное в примере 1 значение
и найденное в примере 1 значение  . Получим уравнение касательной:
. Получим уравнение касательной:  и уравнение нормали:
и уравнение нормали:

 – уравнение касательной;
– уравнение касательной; – уравнение нормали.
– уравнение нормали. в точках
в точках 
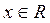 , пользуясь определением. Зададим аргументу приращение
, пользуясь определением. Зададим аргументу приращение  и найдем соответствующее ему приращение функции:
и найдем соответствующее ему приращение функции: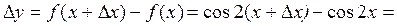


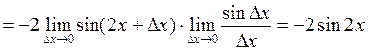
 . Вычислим значения производной в указанных точках:
. Вычислим значения производной в указанных точках:




 то скорость движения v в момент времени t 0 есть производная по времени:
то скорость движения v в момент времени t 0 есть производная по времени:  , а ускорение а в момент времени t 0 определяется производной скорости движения по времени:
, а ускорение а в момент времени t 0 определяется производной скорости движения по времени: 
 в точке
в точке  , соответствующее приращению аргумента
, соответствующее приращению аргумента 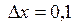 .
. в точке
в точке  , соответствующее приращению аргумента
, соответствующее приращению аргумента 
 в точке
в точке  для любого приращения аргумента
для любого приращения аргумента 
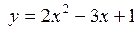 в точке x = 2 для любого приращения аргумента
в точке x = 2 для любого приращения аргумента  для функции
для функции 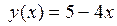 .
. для функции
для функции  в любой точке,
в любой точке,  и найти значения этой производной в точках:
и найти значения этой производной в точках: 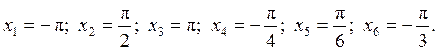
 в любой точке,
в любой точке, 
 в точке M (2;2), составить уравнения касательной и нормали к этой кривой в точке M, сделать чертеж.
в точке M (2;2), составить уравнения касательной и нормали к этой кривой в точке M, сделать чертеж. найти точку, касательная к которой параллельна биссектрисе первого координатного угла. Составить уравнение этой касательной. Сделать чертеж.
найти точку, касательная к которой параллельна биссектрисе первого координатного угла. Составить уравнение этой касательной. Сделать чертеж. найти точку, касательная к которой перпендикулярна прямой
найти точку, касательная к которой перпендикулярна прямой  . Составить уравнение этой касательной. Сделать чертеж.
. Составить уравнение этой касательной. Сделать чертеж. , приходящих через точку A (2;2). Сделать чертеж.
, приходящих через точку A (2;2). Сделать чертеж. где S – расстояние в метрах, t – время в секундах. Найти скорость этой точки в момент времени t = 4.
где S – расстояние в метрах, t – время в секундах. Найти скорость этой точки в момент времени t = 4.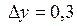 ; 3.2.
; 3.2.  ; 3.3.
; 3.3. 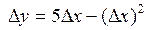 ; 3.4.
; 3.4. 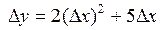 ;
;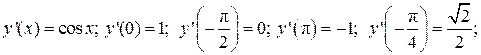
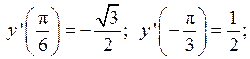 3.8.
3.8. 

 – уравнение касательной;
– уравнение касательной;  – уравнение нормали; 3.10.
– уравнение нормали; 3.10.  – уравнение касательной;
– уравнение касательной;  – уравнение нормали; 3.11.
– уравнение нормали; 3.11.  – точка касания;
– точка касания;  – уравнение касательной; 3.12.
– уравнение касательной; 3.12. 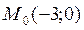 – точка касания;
– точка касания;  – уравнение касательной; 3.13.
– уравнение касательной; 3.13.  ; 3.14.
; 3.14.  .
.


