
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Направление выпуклости графика функции. Точки перегиба
График функции y = f (x)называется выпуклым вверх (выпуклым) на интервале (a; b) если в пределах этого интервала график функции y = f (x) лежит ниже любой своей касательной. График функции y = f (x) называется выпуклым вниз (вогнутым) на интервале (a; b) если в пределах этого интервала график функции y = f (x) лежит выше любой своей касательной. Точка графика функции y = f (x) M0 (x0; f (x0))называется точкой перегиба графика, если при переходе x через x 0график меняет направление выпуклости. Пусть функция y = f (x) дважды дифференцируема на интервале (a;b), тогда если в каждой точке этого интервала Если точка M0 (x0; f (x0))является точкой перегиба графика функции y=f (x), то Точка x0 области определения функции, в которой вторая производная функции обращается в ноль или не существует, называется критической точкой II рода. Для того чтобы точка M0 (x0; f (x0))графика функции y=f (x) была точкой перегиба, достаточно, чтобы существовала конечная Пример 1. Найти интервалы выпуклости, вогнутости и точки перегиба графика функции Решение.
Находим критические точки II рода: а) б)
Вычислим
Получим Ответ: Пример 2. Найти интервал выпуклости, вогнутости и точки перегиба графика функции Решение.
Находим критические точки II рода: а) б)
Вычислим Получим Ответ:
Примеры для самостоятельного решения Найти интервалы выпуклости, вогнутости и точки перегибы следующих функций: 13.1. 13.2. 13.3. 13.4. 13.5. 13.6. 13.7. 13.8. 13.9. 13.10
Ответы 13.1. 13.2. 13.3.
13.4. 13.5. 13.6. 13.7. 13.8. 13.9. 13.10. Асимптоты графика функции Прямая l называется асимптотой кривой y = f (x), если расстояние от точки M (x; y) кривой до прямой l стремится к нулю при неограниченном удалении этой точки по кривой от начала координат (т.е. при стремлении хотя бы одной из координат точки к бесконечности). Прямая x = a является вертикальной асимптотой кривой y = f(x), если выполняется хотя бы одно из условий:
Прямая y = k x + b наклонная асимптота кривой y=f (x) при
Частный случай наклонной асимптоты при Примеры с решениями Пример 1. Найти асимптоты графика функции Решение. Область определения
Рассмотрим Наклонная асимптота: y = k x + b, где k и b находим по формулам (2)
Получили k = 3 и b = 5, следовательно, наклонная асимптота имеет уравнение y = 3 x + 5. Ответ: x = 2; y = 3 x + 5. Пример 2. Найти асимптоты графика функции Решение. Наклонная асимптота: y = k x + b, где k и b находим по формулам (2).
Получили k = 0 и b = 3, следовательно, прямая y = 3 является горизонтальной асимптотой графика рассматриваемой функции. Ответ: y = 3.
Пример 3. Найти асимптоты графика функции Решение. Наклонная асимптота: y = k x + b, где k и b находим по формулам (2).
Получили k = 0 и b = 0 при Ответ: y = 0 (при
Примеры для самостоятельного решения Найти асимптоты графиков следующих функций: 14.1. 14.2. 14.3. 14.4. 14.5. 14.6. 14.7.
14.8.
14.9. 14.10.
14.11.
14.12.
Ответы 14.1. 14.2. 14.3. 14.4. 14.5. 14.6. 14.7. 14.8. 14.9. 14.10. 14.11. 14.12.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.236.219 (0.027 с.) |
 , то график функции на (a; b) выпуклый вверх (выпуклый), а если
, то график функции на (a; b) выпуклый вверх (выпуклый), а если  , то график функции на (a; b) выпуклый вниз (вогнутый). Это достаточные условия выпуклости (вогнутости) графика.
, то график функции на (a; b) выпуклый вниз (вогнутый). Это достаточные условия выпуклости (вогнутости) графика. или
или  не существует – необходимое условие точки перегиба.
не существует – необходимое условие точки перегиба. в некоторой окрестности точки x0 (за исключением, может быть, самой точки x0) и чтобы
в некоторой окрестности точки x0 (за исключением, может быть, самой точки x0) и чтобы  .
.

 не существует:
не существует:  ,
, при
при 



 и
и  − точки перегиба.
− точки перегиба. – интервалы вогнутости,
– интервалы вогнутости,  − интервал выпуклости,
− интервал выпуклости,  и
и  − точки перегиба.
− точки перегиба.

 не существует при
не существует при  ,
, :
: 

 − точка перегиба.
− точка перегиба. − интервалы выпуклости,
− интервалы выпуклости,  − интервал вогнутости,
− интервал вогнутости,  − точка перегиба.
− точка перегиба. ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
;
 − интервал выпуклости,
− интервал выпуклости,  − интервал вогнутости,
− интервал вогнутости,  − точка перегиба;
− точка перегиба; − интервал выпуклости,
− интервал выпуклости,  − интервал вогнутости,
− интервал вогнутости,  − точка перегиба.
− точка перегиба. − интервалы выпуклости,
− интервалы выпуклости,  − интервалы вогнутости,
− интервалы вогнутости,  − точки перегиба.
− точки перегиба. − интервал выпуклости,
− интервал выпуклости,  − интервал вогнутости, точек перегиба нет.
− интервал вогнутости, точек перегиба нет. − интервалы вогнутости,
− интервалы вогнутости,  − интервал выпуклости,
− интервал выпуклости,  − точки перегиба.
− точки перегиба. − интервалы выпуклости,
− интервалы выпуклости,  − интервалы вогнутости,
− интервалы вогнутости,  − точки перегиба.
− точки перегиба.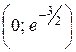 − интервал выпуклости,
− интервал выпуклости,  − интервал вогнутости,
− интервал вогнутости, 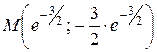 − точка перегиба.
− точка перегиба. − точка перегиба.
− точка перегиба. − интервалы вогнутости,
− интервалы вогнутости, 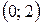 − интервал выпуклости,
− интервал выпуклости,  − точка перегиба.
− точка перегиба. − интервалы вогнутости,
− интервалы вогнутости,  − точки перегиба.
− точки перегиба. (1)
(1) (при
(при  ), если выполнены условия:
), если выполнены условия: (2)
(2) – горизонтальная асимптота y = b.
– горизонтальная асимптота y = b.

 − точка разрыва графика функции, через нее может проходить вертикальная асимптота.
− точка разрыва графика функции, через нее может проходить вертикальная асимптота. , следовательно, и выполнено одно из условий (1) и прямая
, следовательно, и выполнено одно из условий (1) и прямая  является вертикальной асимптотой.
является вертикальной асимптотой.
 .
.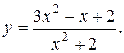
 Область определения функции не имеет точек разрыва, следовательно, вертикальных асимптот нет.
Область определения функции не имеет точек разрыва, следовательно, вертикальных асимптот нет.


 вертикальных асимптот нет.
вертикальных асимптот нет. , следовательно, при
, следовательно, при  наклонной асимптоты нет.
наклонной асимптоты нет.
 , это значит, что прямая y = 0 является горизонтальной асимптотой при
, это значит, что прямая y = 0 является горизонтальной асимптотой при 
 ;
;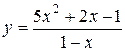 ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; ;
; .
. ;
; ;
; ;
; ;
; ;
;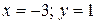 ;
; ;
; ;
; ;
; ;
; ;
; .
.


