
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное и интегральное исчисление функции одной переменнойСтр 1 из 10Следующая ⇒
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ (ПРИМЕРЫ И ЗАДАЧИ)
Утверждено Редакционным советом университета в качестве учебного пособия
Москва УДК 517 (075) ББК 22.161.1 Д50
Авторы: Е. Г. Рудаковская, О. В. Аверина, C. М. Воронов, Т. Н. Старшова, Т. В. Хлынова, Т. В. Ригер
Рецензенты: Доктор физико-математических наук, профессор Российского химико-технологического университета имени Д. И. Менделеева В. М. Аристов Доктор технических наук, профессор Российского химико-технологического университета имени Д. И. Менделеева Л. С. Гордеев
Дифференциальное и интегральное исчисление функции одной пере- Д50 менной (примеры и задачи): учеб. пособие / Е. Г. Рудаковская, О. В. Аверина, С. М. Воронов, Т. Н. Старшова, Т. В. Хлынова, Т. В. Ригер; под ред. Е. Г. Рудаковской. – М.: РХТУ им. Д. И. Менделеева, 2013. – 132 с. ISBN 978-5-7237-1114-3
Пособие представляет курс практических занятий по математическому анализу, проводимых кафедрой высшей математики РХТУ им. Д. И. Менделеева. Охватывает следующие разделы курса математического анализа: теория пределов, дифференциальное исчисление функций одной переменной, интегральное исчисление функций одной переменной. В каждом параграфе изложены теоретические основы, необходимые для решения практических задач, примеры с подобранным решением, задачи для самостоятельного решения с ответами. Большое внимание уделено разбору примеров по изучаемым темам, имеющим прикладное значение для других дисциплин. Предназначено для студентов I курса всех факультетов и колледжей РХТУ им. Д. И. Менделеева.
УДК 517 (075) ББК 22.161.1
ISBN 978-5-7237-1114-3 © Российский химико-технологический университет им. Д. И. Менделеева, 2013 Оглавление Глава 1. Дифференциальное исчисление функции одной переменной….………4 §1. Предел функции. Вычисление предела функции с помощью алгебраических преобразований…………………………………………………………..……….4 §2. Вычисление предела функции с использованием замечательных пределов………………………………………………………………………....10 §3. Производная функции одной переменной (определение, геометрический смысл)…………………………………………………..………………………..13 §4. Дифференцирование по формулам, правила дифференцирования ……………………………………………………………..………………..……19
§5. Производная сложной функции………………………………………..….23 §6. Дифференцирование функций, заданных неявно…………………..…….27 §7. Дифференцирование функций, заданных параметрически………….…..33 §8. Дифференциал функции……………………………………………..…….37 §9. Производные и дифференциалы высших порядков…………………..….42 §10. Раскрытие неопределённостей. Правило Лопиталя……………..………49 §11. Возрастание и убывание функции. Экстремумы функции…………..…56 §12. Наименьшее и наибольшее значение функции, непрерывной на отрезке……………………………………………………………………......61 §13. Направление выпуклости графика функции. Точки перегиба………...65 §14. Асимптоты графика функции………………………………………….…68 §15. Исследование функции и построение её графика…………………..…...71 Глава 2. Интегральное исчисление функции одной переменной.................…..79 §1. Первообразная функция и неопределенный интеграл......................…….79 §2. Интегрирование посредством разложения подынтегральной функции на слагаемые…………………………………………………………….………85 §3. Интегрирование подстановкой …………………………………….……...87 §4. Интегрирование по частям……………………………………..…………..90 §5. Интегрирование рациональных дробей………………………………..….96 §6. Интегрирование тригонометрических выражений…………………..….102 §7. Интегрирование некоторых видов иррациональных выражений….…...107 §8. Определённый интеграл……………………..…………………………....112 §9. Приложения определенного интеграла……………………..……….......118 §10. Несобственные интегралы…………………………..……………….......126 Примеры с решениями Пример 1. Используя определения, доказать, что функция Решение. Возьмём любое
Односторонние пределы Бывают случаи, когда способ приближения аргумента существенно влияет на значение предела функции. Поэтому вводят понятие односторонних пределов. Определение 3. Число A называется правым (левым) пределом функции При этом записывают:
Свойства конечных пределов Пусть существуют конечные пределы
При вычислении пределов функций можно использовать понятие эквивалентности. Определение 4. Если в некоторой окрестности точки
При этом записывают: Примеры эквивалентных функций при
tg x~x arctg x~x Ответы 1.1. 1.11.
Примеры с решениями Пример 1. Вычислить предел:
Решение. Ответ: a. Пример 2. Вычислить предел:
Решение. Используем тригонометрические формулы:
Ответ: 4.
Вторым замечательным пределом называется предел вида:
Пример 3. Вычислить предел:
Ответ: Пример 4. Вычислить предел:
Решение.
Ответ: Примеры для самостоятельного решения Вычислить пределы:
Ответы 2.1. 5. 2.2. 3. 2.3. 2.19. – 1. 2.20. – 0,5. 2.21.
Примеры с решениями Пример 1. Найти Решение. Пусть
Воспользуемся определением производной:
Ответ: Пример 2. Найти Решение. Пусть
Воспользуемся определением:
Ответ: Заметим, что функция С геометрической точки зрения значение производной функции
Уравнение касательной, проведенной к графику функции
Уравнение нормали к графику той же функции в точке с абсциссой x 0:
если Если в точке x 0 функция
Уравнение касательной в этих случаях имеет вид: x = x 0, а уравнение нормали – Углом между кривыми
если Если же Пример 3. Составить уравнения касательной и нормали к графику функции Решение. Воспользуемся уравнениями касательной (2) и нормали (3).
В эти уравнения надо поставить x 0 = 2;
Ответ:
Пример 4. Пользуясь определением, найти значение производной функции Решение. Выведем формулу производной функции
Итак,
Ответ: Если при прямолинейном движении точки задан закон движения
Примеры для самостоятельного решения 3.1. Вычислить приращение функции 3.2. Вычислить приращение функции 3.3. Найти приращение функции 3.4. Найти приращение функции 3.5. Пользуясь определением производной, вычислить 3.6. Пользуясь определением производной, вычислить 3.7. Пользуясь определением производной, вывести формулу производной функции 3.8. Пользуясь определением производной, вывести формулу производной функции производной в точках:
3.9. Найти угловой коэффициент касательной к графику функции 3.10. Составить уравнения касательной и нормали к графику функции 3.11. На графике функции 3.12. На графике функции 3.13. Составить уравнения касательных к графику функции 3.14. Закон движения точки: Ответы 3.1.
3.5. – 4; 3.6. – 4; 3.7.
3.9.
Примеры с решениями Пример 1. Найти производную функции Решение. Используя правила дифференцирования (2 и 4) и формулу производной степенной функции (3–5), получим
Ответ: Пример 2. Найти производную функции в точке Решение. Воспользуемся правилами дифференцирования (2–4), получим:
Ответ:
Примеры для самостоятельного решения 4.1. 4.2. 4.3. 4.4. 4.5. Найти Сделать чертеж. 4.6. Найти Сделать чертеж. 4.7. Найти Сделать чертеж. 4.8. 4.9. 4.10. 4.11. 4.12. 4.13. 4.14. 4.15. Тело массой 5 кг движется по прямой по закону 4.16. Дан закон прямолинейного движения точки: 4.17. Вывести формулу производной произведения трех дифференцируемых функций. 4.18. 4.19. Под каким углом пересекаются кривые 4.20. Составить уравнение той нормали к кривой Ответы 4.1. 4.2. 4.3. 4.4. 4.5. 4.6. 4.7. 4.8. 4.9. 4.10. 4.11. 4.12. 4.13. 4.14. 4.15. 4.16. 4.17. 4.18. 4.19. 4.20.
Производная сложной функции Если функция
Примеры с решениями Пример 1. Найти производную функции Решение. Обозначим
Ответ: Пример 2. Найти производную функции Решение. Здесь
Ответ: Пример 3. Найти производную функции Решение. Здесь
Ответ Пример 4. Найти производную функции Решение. Перед нами показательно-степенная функция, т.е. функция вида Для ее дифференцирования можно воспользоваться несколькими способами. Один из них мы рассмотрим сейчас, другой будет разобран в параграфе о дифференцировании функций, заданных неявно. Итак, преобразуя заданную показательно-степенную функцию с помощью основного логарифмического тождества, приведем ее к виду показательной функции:
Получили сложную функцию
Ответ: Примеры для самостоятельного решения 5.1. 5.2. 5.3. 5.4. 5.5. 5.6. 5.7. 5.8. 5.9. 5.10. 5.11. 5.12. 5.13. 5.14. 5.15. 5.16. 5.17. 5.18. 5.19. 5.20. 5.21. 5.22. 5.23. 5.24. 5.25. 5.26. 5.27. Составить уравнение той касательной к кривой 5.28. Зависимость между количеством 5.29.
Ответы 5.1. 5.3. 5.4. 5.5. 5.6. 5.8. 5.10. 5.11. 5.12.
5.13. 5.14. 5.15. 5.18.
5.21. 5.23. 5.26. 5.29.
Примеры с решениями Пример 1. Функция Найти Решение. Поскольку у является функцией от х, будем рассматривать y ³ как сложную функцию от х, следовательно,
Ответ:
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.84.32 (0.27 с.) |
 в точке
в точке  имеет предел, равный 5, т.е.
имеет предел, равный 5, т.е.  .
. >0. Задача состоит в том, чтобы для этого
>0. Задача состоит в том, чтобы для этого 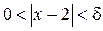 следовало бы неравенство
следовало бы неравенство 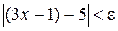 . Преобразуя последнее неравенство, получаем
. Преобразуя последнее неравенство, получаем  , или
, или 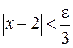 . Отсюда видно, если взять
. Отсюда видно, если взять  , то для всех
, то для всех 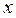 , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется требуемое неравенство
, выполняется требуемое неравенство  . Это и означает, что
. Это и означает, что  .
.
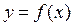 в точке
в точке 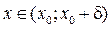
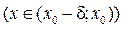
 , выполняется неравенство:
, выполняется неравенство: 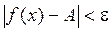 .
.  ,
,  для левого предела.
для левого предела. тогда справедливы следующие равенства:
тогда справедливы следующие равенства: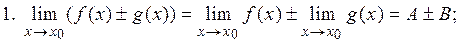
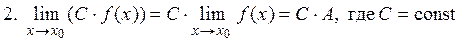

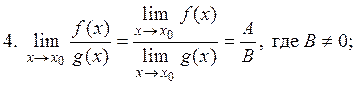

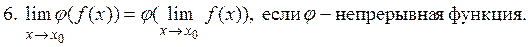
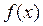 ,
, 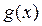 ,
, 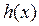 такие, что,
такие, что, 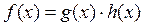 ,
, 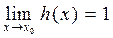 ,то функции
,то функции 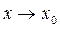 .
.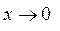 :
: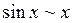
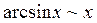
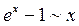
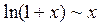
 . 1.2. – 2. 1.3. 14. 1.4. 1. 1.5.
. 1.2. – 2. 1.3. 14. 1.4. 1. 1.5.  . 1.6. –9. 1.7. 3. 1.8.
. 1.6. –9. 1.7. 3. 1.8.  . 1.9.
. 1.9.  . 1.10. 6.
. 1.10. 6. . 1.12.
. 1.12.  1.13.
1.13.  1.14.
1.14.  . 1.16.
. 1.16.  . 1.17.
. 1.17.  . 1.18.
. 1.18.  . 1.19. ∞. 1.20. 0. 1.21. 1. 1.22.
. 1.19. ∞. 1.20. 0. 1.21. 1. 1.22.  . 1.23.
. 1.23.  . 1.24. ∞. 1.25.
. 1.24. ∞. 1.25. 

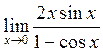



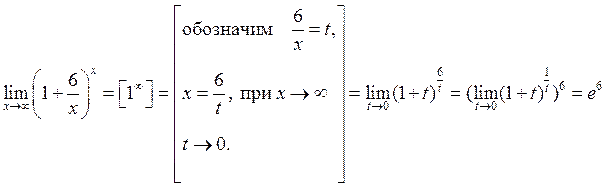
 .
.


 .
.




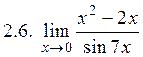






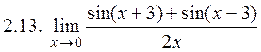



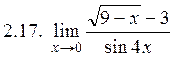





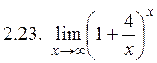








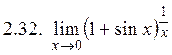

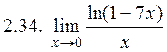
 . 2.4.
. 2.4.  2.5. – 4,5. 2.6. –
2.5. – 4,5. 2.6. –  . 2.7. 0,5. 2.8. 2. 2.9. –
. 2.7. 0,5. 2.8. 2. 2.9. – 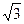 . 2.17. –
. 2.17. –  . 2.18. 14.
. 2.18. 14. . 2.24.
. 2.24.  . 2.25.
. 2.25.  . 2.26.
. 2.26.  . 2.27.
. 2.27.  . 2.28.
. 2.28.  . 2.29.
. 2.29.  . 2.30.
. 2.30. 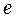 . 2.33. 1. 2.34. –7.
. 2.33. 1. 2.34. –7. для функции
для функции  пользуясь определением производной.
пользуясь определением производной. – приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:
– приращение аргумента. Найдем соответствующие ему приращение функции в точке x = 2:




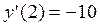
 для функции
для функции  в точке х = 0.
в точке х = 0.
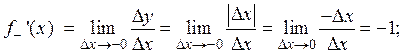

 .
. не имеет производной в точке x= 0, так как
не имеет производной в точке x= 0, так как 
 в точке x 0 представляет собой угловой коэффициент касательной, проведенной к графику функции
в точке x 0 представляет собой угловой коэффициент касательной, проведенной к графику функции  , где
, где  – угол наклона касательной к оси Оx.
– угол наклона касательной к оси Оx.
 . (2)
. (2)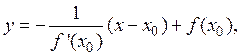 (3)
(3)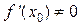 .
. или
или  или
или  , то касательная к графику этой функции в точке с абсциссой x 0 перпендикулярна оси
, то касательная к графику этой функции в точке с абсциссой x 0 перпендикулярна оси 
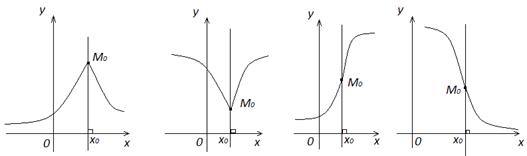
 . Если же
. Если же  , то уравнение нормали: x = x 0.
, то уравнение нормали: x = x 0. и
и  называется угол между касательными, проведёнными к этим кривым в точке их пересечения
называется угол между касательными, проведёнными к этим кривым в точке их пересечения 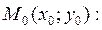
 (4)
(4) .
. , то касательные перпендикулярны и
, то касательные перпендикулярны и  .
. в точке с абсциссой x 0 = 2.
в точке с абсциссой x 0 = 2. и найденное в примере 1 значение
и найденное в примере 1 значение  . Получим уравнение касательной:
. Получим уравнение касательной:  и уравнение нормали:
и уравнение нормали:

 – уравнение касательной;
– уравнение касательной; – уравнение нормали.
– уравнение нормали. в точках
в точках 
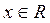 , пользуясь определением. Зададим аргументу приращение
, пользуясь определением. Зададим аргументу приращение  и найдем соответствующее ему приращение функции:
и найдем соответствующее ему приращение функции: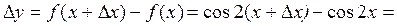


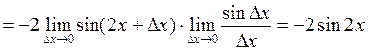
 . Вычислим значения производной в указанных точках:
. Вычислим значения производной в указанных точках:




 то скорость движения v в момент времени t 0 есть производная по времени:
то скорость движения v в момент времени t 0 есть производная по времени:  , а ускорение а в момент времени t 0 определяется производной скорости движения по времени:
, а ускорение а в момент времени t 0 определяется производной скорости движения по времени: 
 в точке
в точке  , соответствующее приращению аргумента
, соответствующее приращению аргумента 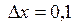 .
. в точке
в точке  , соответствующее приращению аргумента
, соответствующее приращению аргумента 
 в точке
в точке  для любого приращения аргумента
для любого приращения аргумента 
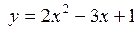 в точке x = 2 для любого приращения аргумента
в точке x = 2 для любого приращения аргумента  для функции
для функции 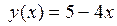 .
. для функции
для функции  в любой точке,
в любой точке,  и найти значения этой производной в точках:
и найти значения этой производной в точках: 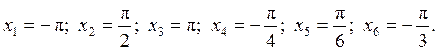
 в любой точке,
в любой точке, 
 в точке M (2;2), составить уравнения касательной и нормали к этой кривой в точке M, сделать чертеж.
в точке M (2;2), составить уравнения касательной и нормали к этой кривой в точке M, сделать чертеж. найти точку, касательная к которой параллельна биссектрисе первого координатного угла. Составить уравнение этой касательной. Сделать чертеж.
найти точку, касательная к которой параллельна биссектрисе первого координатного угла. Составить уравнение этой касательной. Сделать чертеж. найти точку, касательная к которой перпендикулярна прямой
найти точку, касательная к которой перпендикулярна прямой  . Составить уравнение этой касательной. Сделать чертеж.
. Составить уравнение этой касательной. Сделать чертеж. , приходящих через точку A (2;2). Сделать чертеж.
, приходящих через точку A (2;2). Сделать чертеж. где S – расстояние в метрах, t – время в секундах. Найти скорость этой точки в момент времени t = 4.
где S – расстояние в метрах, t – время в секундах. Найти скорость этой точки в момент времени t = 4.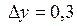 ; 3.2.
; 3.2.  ; 3.3.
; 3.3. 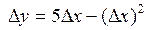 ; 3.4.
; 3.4. 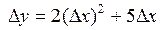 ;
;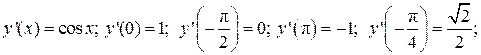
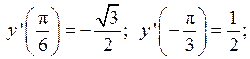 3.8.
3.8. 

 – уравнение касательной;
– уравнение касательной;  – уравнение нормали; 3.10.
– уравнение нормали; 3.10.  – уравнение касательной;
– уравнение касательной;  – уравнение нормали; 3.11.
– уравнение нормали; 3.11.  – точка касания;
– точка касания;  – уравнение касательной; 3.12.
– уравнение касательной; 3.12. 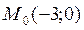 – точка касания;
– точка касания;  – уравнение касательной; 3.13.
– уравнение касательной; 3.13.  ; 3.14.
; 3.14.  .
.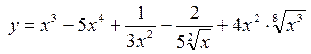 в точке
в точке 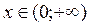 .
.

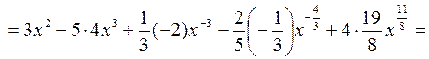

 .
.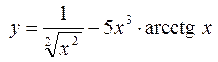

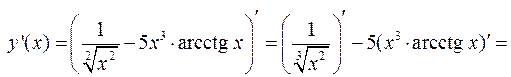
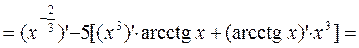


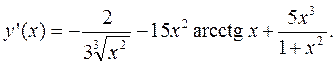
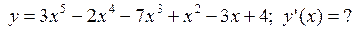


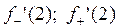 , если
, если 
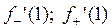 , если
, если 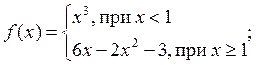
 , если
, если 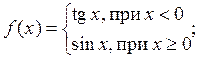
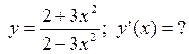
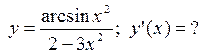



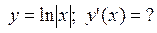

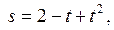 где t – время (с), s – путь (см). Вычислить кинетическую энергию
где t – время (с), s – путь (см). Вычислить кинетическую энергию  этого тела в конце 3-й секунды.
этого тела в конце 3-й секунды.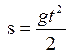 , где t – время в секундах,
, где t – время в секундах, 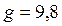 . Найти скорость в конце 2-й и в конце 5-й секунды.
. Найти скорость в конце 2-й и в конце 5-й секунды.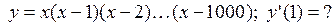
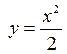 и
и 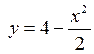
 , которая перпендикулярна прямой
, которая перпендикулярна прямой  . Сделать чертеж.
. Сделать чертеж.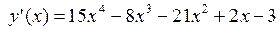 ;
;




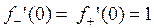
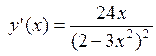
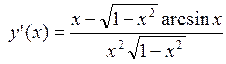

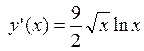

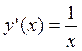
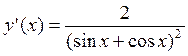

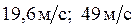
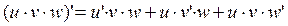
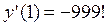
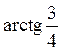
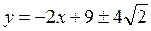
 дифференцируема в точке
дифференцируема в точке 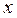 , а функция
, а функция 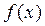 дифференцируема в соответствующей точке
дифференцируема в соответствующей точке 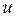 , то сложная функция
, то сложная функция 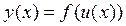 дифференцируема в точке
дифференцируема в точке 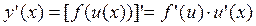 .
. .
.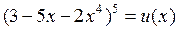 , тогда
, тогда  . По правилу дифференцирования сложной функции получаем
. По правилу дифференцирования сложной функции получаем
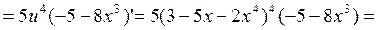
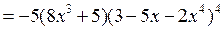
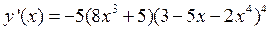 .
. .
.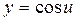 ,где
,где 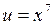
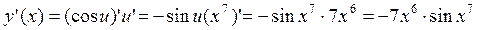
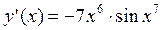
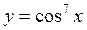 .
. , где
, где 
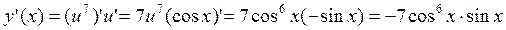
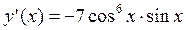
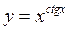 где
где 
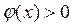 .
.
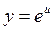 , где
, где 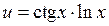
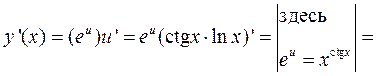
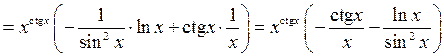
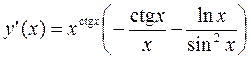
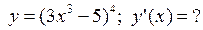
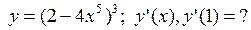


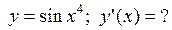
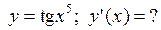
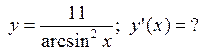
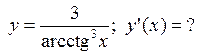
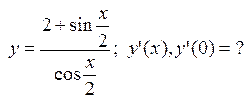
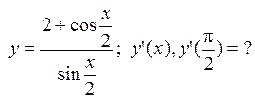
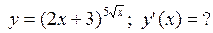
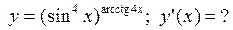


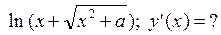
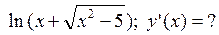
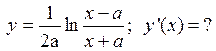

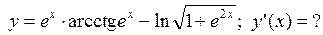



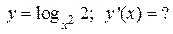


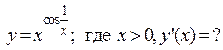
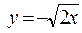 , которая перпендикулярна прямой
, которая перпендикулярна прямой  . Сделать чертеж.
. Сделать чертеж.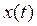 вещества, получаемого в некоторой химической реакции, временем t выражается уравнением:
вещества, получаемого в некоторой химической реакции, временем t выражается уравнением: 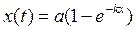 . Определить скорость реакции.
. Определить скорость реакции.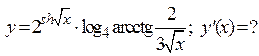
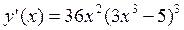 ; 5.2.
; 5.2. 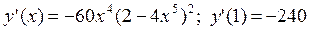 ;
;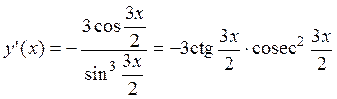 ;
; ;
;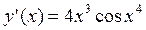 ;
; ; 5.7.
; 5.7. 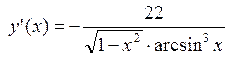 ;
; ; 5.9.
; 5.9. 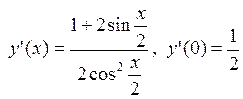 ;
;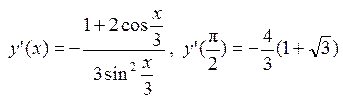 ;
;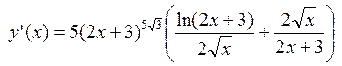 ;
; ;
;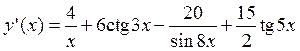 ;
;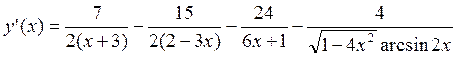 ;
;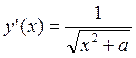 ; 5.16.
; 5.16. 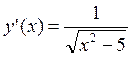 ; 5.17.
; 5.17.  ;
; ; 5.19.
; 5.19.  ; 5.20.
; 5.20.  ;
; ; 5.22.
; 5.22. 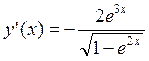 ;
;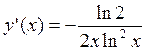 ; 5.24.
; 5.24. 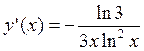 ; 5.25.
; 5.25.  ;
;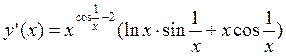 ; 5.27.
; 5.27. 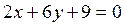 ; 5.28.
; 5.28. 


 .
. задана неявно уравнением
задана неявно уравнением 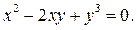
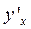 .
.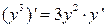 . Продифференцировав по х обе части заданного уравнения, получим:
. Продифференцировав по х обе части заданного уравнения, получим:


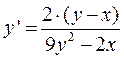 .
.


