
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раскрытие неопределённостей. Правило Лопиталя
При решении задач, связанных с вычислением пределов функций, часто непосредственная подстановка предельного значения аргумента приводит к неопределённым выражениям вида: Теорема. Если функции 1) 2) 3) существует (конечный или бесконечный)
Замечание 1. Если Замечание 2. Правилом Лопиталя можно пользоваться (в случае выполнения условий теоремы) при раскрытии неопределенностей вида Замечание 3. Правило Лопиталя в некоторых задачах можно применять повторно. Если необходимо раскрыть неопределенности иного вида, нежели Если при
Если при
Иногда удобно пользоваться и другими преобразованиями:
При вычислении пределов вида
Тогда (в силу непрерывности показательной функции) получают: Примеры с решениями Пример 1. Вычислить Решение. Подстановка предельного значения аргумента
Ответ: Пример 2. Вычислить Решение.
Ответ: Пример 3. Вычислить Решение.
Ответ: 0 Пример 4. Вычислить Решение.
Ответ: Пример 5. Вычислить Решение.
Ответ: Пример 6. Вычислить Решение. Рассмотрим
Ответ: Пример 7. Вычислить Решение. Перед нами неопределенность
Ответ: 1. Пример 8. Вычислить Решение. Правило Лопиталя не применимо, так как при
Ответ: Пример 9. Вычислить Решение.
Правило Лопиталя не приводит нас к решению этой задачи, но искомый предел существует и его легко вычислить, разделив числитель и знаменатель дроби на x:
Ответ: Примеры для самостоятельного решения Вычислить следующие пределы: 10.1. 10.2. 10.3. 10.4. 10.5. 10.6. 10.7. 10.8. 10.9. 10.10. 10.11. 10.12. 10.13. 10.14. 10.15. 10.16. 10.17. 10.18. 10.19. 10.20. 10.21. Ответы 10.1.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.198 (0.019 с.) |
 Нахождение предела в таких случаях называют раскрытием соответствующей неопределенности. Довольно часто справиться с этой проблемой помогает так называемое правило Лопиталя, которое можно сформулировать в виде теоремы.
Нахождение предела в таких случаях называют раскрытием соответствующей неопределенности. Довольно часто справиться с этой проблемой помогает так называемое правило Лопиталя, которое можно сформулировать в виде теоремы. и
и  удовлетворяют следующим условиям:
удовлетворяют следующим условиям: или
или  ;
; и
и  дифференцируемы в некоторой окрестности точки
дифференцируемы в некоторой окрестности точки  , и
, и  для любого
для любого  их этой окрестности (за исключением, может быть, самой точки
их этой окрестности (за исключением, может быть, самой точки  );
); , то тогда
, то тогда .
. может существовать, а может и не существовать. В такой ситуации решать задачу вычисления предела надо без использования правила Лопиталя.
может существовать, а может и не существовать. В такой ситуации решать задачу вычисления предела надо без использования правила Лопиталя.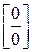 или
или  не только при
не только при  , но и при
, но и при  .
.
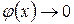 , а
, а  , то вычисление предела
, то вычисление предела  (неопределенность вида
(неопределенность вида  ) может быть сведено к одному из случаев
) может быть сведено к одному из случаев  или
или 
 , а
, а  , то вычисление предела
, то вычисление предела  (неопределенность вида
(неопределенность вида  ) может быть сведено к раскрытию неопределенности
) может быть сведено к раскрытию неопределенности  путем тождественного преобразования разности в произведение:
путем тождественного преобразования разности в произведение: .
. или
или 
 можно столкнуться с неопределенностью
можно столкнуться с неопределенностью  или
или  , или
, или  . Раскрытие этих неопределенностей производят с помощью следующего преобразования:
. Раскрытие этих неопределенностей производят с помощью следующего преобразования: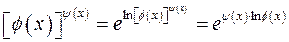
 , что сводит задачу к неопределенности
, что сводит задачу к неопределенности  .
.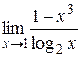
 приводит к неопределенности
приводит к неопределенности  и
и  . Второе условие теоремы тоже выполняется, поскольку функции
. Второе условие теоремы тоже выполняется, поскольку функции  и
и  дифференцируемы в некоторой окрестности точки
дифференцируемы в некоторой окрестности точки  для любого
для любого  ). Выполняется и третье условие: существует предел отношения производных этих функций
). Выполняется и третье условие: существует предел отношения производных этих функций  . Итак, решение этой задачи можно коротко записать следующим образом:
. Итак, решение этой задачи можно коротко записать следующим образом:












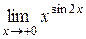




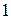 .
.
 не имеет предела при
не имеет предела при  . Однако, это не значит, что исходный предел не существует, его можно вычислить без использования правила Лопиталя, применяя лишь тождественные преобразования и свойства пределов:
. Однако, это не значит, что исходный предел не существует, его можно вычислить без использования правила Лопиталя, применяя лишь тождественные преобразования и свойства пределов: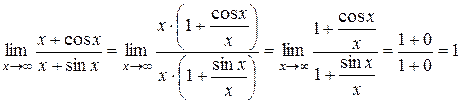

 предел отношения производных
предел отношения производных  не существует. Но задача имеет решение:
не существует. Но задача имеет решение:










 где
где 


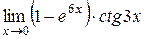











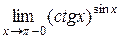

 ; 10.2.
; 10.2.  ; 10.3.
; 10.3.  ; 10.4.
; 10.4. 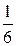 ; 10.7.
; 10.7.  ; 10.9.
; 10.9.  ; 10.10.
; 10.10.  ; 10.13.
; 10.13.  ; 10.15.
; 10.15.  ; 10.16.
; 10.16.  ; 10.17.
; 10.17.  ; 10.19.
; 10.19.  ; 10.20.
; 10.20. 


