
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наименьшее и наибольшее значение функции, непрерывной на отрезкеСодержание книги
Поиск на нашем сайте
Непрерывная на отрезке функция достигает на этом отрезке своих наибольшего и наименьшего значений (теорема Вейерштрасса). Эти значения функция может принимать либо в точках экстремума, находящихся внутри рассматриваемого отрезка, либо на концах этого отрезка. Поэтому решать задачу на наибольшее и наименьшее значения функции на отрезке можно, руководствуясь следующим правилом: 1) найти критические точки функции, принадлежащие интервалу 2) вычислить значения функции в найденных критических точках и на концах отрезка 3) из полученных значений выбрать наибольшее и наименьшее. Замечание 1. Если функция имеет внутри отрезка лишь одну критическую точку, которая является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение. Замечание 2. Если функция внутри отрезка не имеет критических точек, то это означает, что она строго монотонна на всем этом отрезке и своих наибольшего и наименьшего значений достигает в концах отрезка. Примеры с решениями Пример 1. Найти наименьшее и наибольшее значения функции Решение. Находим
Из полученного следует, что Ответ: наименьшее значение Пример 2. Имеется смесь, состоящая из двух газов: оксида азота и кислорода. При какой концентрации кислорода содержащийся в смеси оксид азота окисляется с максимальной скоростью? Решение. При наличии условий критической необратимости можно считать, что скорость реакции Найдем вторую производную: Ответ: При концентрации кислорода 33,3 %. Пример 3. Требуется изготовить фильтр путём вырезания из круга радиуса
Решение. Обозначим угол сектора через фильтра где Поэтому Итак,
По смыслу задачи ясно, что при
Ответ: при
Примеры для самостоятельного решения Найти наибольшее и наименьшее значения функций на указанных отрезках: 12.1. 12.2. 12.3. 12.4. 12.5. 12.6. 12.7. 12.8. Какова должна быть сторона основания правильной треугольной призмы объёма 12.9.Каковы должны быть радиус основания и высота прямого кругового цилиндра объёма 12.10. Из квадратного жестяного листа, сторона которого 12.11. Из круга радиуса 12.12. Разделить число 10 на такие две части, чтобы сумма их квадратов была наименьшей. 12.13. Найти высоту прямого кругового конуса с наибольшей боковой поверхностью, который можно вписать в данный шар радиуса 12.14. Найти высоту прямого кругового конуса с наименьшим объёмом описанного около шара радиуса 12.15. Найти измерения прямоугольника наибольшей площади, вписанного в эллипс 12.16. Принимая, что прочность бруска с прямоугольным поперечным сечением прямо пропорциональна ширине и кубу высоты, найти ширину бруска наибольшей прочности, который можно вырезать из бревна, диаметр которого равен 16 см. 12.17. Газ, содержащий оксид
12.18. Лампа висит над центром круглого стола радиуса 12.19. Из круглого бревна диаметра а) на сжатие; б) на изгиб? (Сопротивление балки на сжатие пропорционально площади её поперечного сечения, а на изгиб − произведению ширины этого сечения на квадрат его высоты). 12.20. Определить, при каком диаметре
где Ответы 12.1.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.239.70 (0.009 с.) |

 ;
; ;
; на отрезке
на отрезке  .
. . Отсюда видим, что критические точки:
. Отсюда видим, что критические точки: 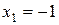 и
и  . Находим значения функции в этих точках и на концах данного отрезка:
. Находим значения функции в этих точках и на концах данного отрезка: .
. − наименьшее, а
− наименьшее, а  − наибольшее значение функции на заданном отрезке.
− наибольшее значение функции на заданном отрезке. , наибольшее значение
, наибольшее значение  выражается формулой
выражается формулой 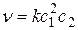 , где
, где  – концентрация
– концентрация 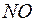 в момент времени
в момент времени  ;
;  – концентрация
– концентрация  ;
;  – константа скорости, зависящая только от температуры. Выражая концентрации
– константа скорости, зависящая только от температуры. Выражая концентрации 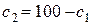 ,
,  . Находим первую производную
. Находим первую производную 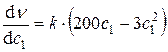 и, приравнивая её к нулю:
и, приравнивая её к нулю: 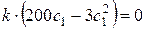 . Найдём
. Найдём  .
. , так как
, так как  , то заключаем, что при
, то заключаем, что при  скорость окисление имеет максимум. Далее, так как при
скорость окисление имеет максимум. Далее, так как при  , то заключаем, что скорость окисления азота имеет максимум, если кислорода в газовой смеси содержится 33,3 %.
, то заключаем, что скорость окисления азота имеет максимум, если кислорода в газовой смеси содержится 33,3 %. сектора и свёртывания последнего в конус. При каком центральном угле сектора объём фильтра будет наибольшим?
сектора и свёртывания последнего в конус. При каком центральном угле сектора объём фильтра будет наибольшим?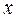 , а радиус окружности основания конуса через
, а радиус окружности основания конуса через  . Тогда
. Тогда  , откуда
, откуда  . Если высота
. Если высота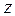 , то объём его
, то объём его 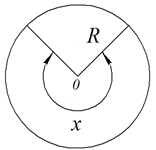
 ,
, или
или  .
. .
. − функция от
− функция от 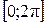 нужно найти. Находим первую производную и приравняем её к нулю:
нужно найти. Находим первую производную и приравняем её к нулю:
 , если
, если  , откуда, рассматривая только то решение, которое имеет смысл, находим
, откуда, рассматривая только то решение, которое имеет смысл, находим 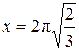 .
.
 на отрезке
на отрезке  .
. на отрезке
на отрезке  .
. на отрезке
на отрезке  и на отрезке
и на отрезке  .
. на отрезке
на отрезке  .
. на отрезке
на отрезке  .
.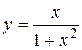 на отрезке
на отрезке 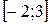 .
. на отрезке
на отрезке  .
. , чтобы её полная поверхность была наименьшей?
, чтобы её полная поверхность была наименьшей?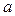 , желают сделать открытый сверху ящик наибольшего объёма, вырезая равные квадраты по углам, удаляя их и затем загибая. Какова должна быть длина сторон у вырезаемых квадратов?
, желают сделать открытый сверху ящик наибольшего объёма, вырезая равные квадраты по углам, удаляя их и затем загибая. Какова должна быть длина сторон у вырезаемых квадратов? . Из этого сектора свёрнута коническая поверхность (прямой круговой конус). При каком
. Из этого сектора свёрнута коническая поверхность (прямой круговой конус). При каком  .
. требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление:
требуется вырезать балку прямоугольного сечения. Каковы должны быть ширина и высота этого сечения, чтобы балка оказывала наибольшее сопротивление: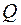 будет иметь наибольшее значение, если
будет иметь наибольшее значение, если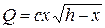 ,
, постоянная, равная глубине низшей точки отверстия, а
постоянная, равная глубине низшей точки отверстия, а  эмпирический коэффициент пропорциональности.
эмпирический коэффициент пропорциональности. при
при  ;
;  при
при  ; 12.2.
; 12.2. 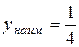 при
при 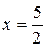 ;
;  при
при  при
при  ;
; 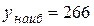 при
при  , б)
, б) 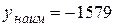 при
при  ;
;  при
при  ; 12.4.
; 12.4.  при
при  ;
; 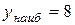 при
при  при
при  ;
; 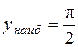 при
при  ; 12.6.
; 12.6.  при
при  при
при  при
при 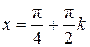 ;
;  ; 12.8.
; 12.8.  ; 12.9. Высота цилиндра и диаметр основания равны; 12.10.
; 12.9. Высота цилиндра и диаметр основания равны; 12.10.  ; 12.11.
; 12.11.  ; 12.12. 5 и 5; 12.14.
; 12.12. 5 и 5; 12.14.  ; 12.15.
; 12.15.  ; 12.16. 8 см; 12.17. 7 %; 12.18.
; 12.16. 8 см; 12.17. 7 %; 12.18.  ; 12.19. а)
; 12.19. а)  и
и  и
и  ; 12.20.
; 12.20. 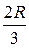 .
.


