
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцирование функций, заданных неявно
Если у есть функция от х и при этом все соответствующие друг другу действительные значения х и у удовлетворяют уравнению Примеры с решениями Пример 1. Функция Найти Решение. Поскольку у является функцией от х, будем рассматривать y ³ как сложную функцию от х, следовательно,
Ответ: Пример 2. Найти производную функции Решение. В данном примере при нахождении производной удобно от явного задания функции перейти к неявному. Прологарифмируем обе части равенства, задающего функцию (при этом обычно используют натуральный логарифм):
Используя свойства логарифмов, позволяющее показатель степени вынести множителем за знак логарифма, получим неявно заданную функцию у в форме, удобной для дифференцирования:
Продифференцируем по х обе части полученного уравнения.
Выразим y ′, домножив обе части этого уравнения на
Ответ: Производную от логарифма функции называют логарифмической производной. Пример 3. Найти производную функции
Решение. Отметим, что данная функция на своей области определения
из этого равенства найдём
Ответ: Пусть у есть функция от аргумента x:
Задавая значения И для всех допустимых значений у будет выполняться равенство
которое можно рассматривать как уравнение, задающее функцию Для вычисления производной функции
Откуда Таким образом, для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции. Пример 4. Вывести формулу производной функции Решение. Рассмотрим функцию Обратная к ней функция имеет вид
Поскольку cos y > 0 для всех
т.е. Ответ: Пример 5. Вывести формулу производной функции, обратной к функции Решение. Дана функция Уравнение Из соотношения Таким образом, Итак, формула производной функции, обратной к гиперболическому синусу, имеет вид:
Ответ:
Примеры для самостоятельного решения Найти производную 6.1. 6.2. 6.3. 6.4. 6.5. 6.6. 6.7. 6.8. Доказать, что функция y (x), заданная неявно уравнением Продифференцировать функции, используя логарифмическую производную: 6.9. 6.10. 6.11. 6.12. 6.13. 6.14. 6.15. Составить уравнения касательной и нормали к графику функции y = y (x) в точке M0 (1;1), если функция задана уравнением 6.16. Составить уравнения касательной и нормали к графику функции y=y (x) в точке M0=(–2; 1), если функция задана уравнением
Найти производные функций, обратных к заданным: 6.17. 6.18. 6.19. 6.20. 6.21. 6.22. Составить уравнения касательных к графику функции 6.23. Составить уравнения касательных к графику функции Ответы 6.1.
6.9. 6.10. 6.11. 6.12. 6.13. 6.14. 6.15. 6.17. 6.19. 6.22.
|
||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.154.103 (0.057 с.) |
 , то говорят, что функция y (x) задана уравнением
, то говорят, что функция y (x) задана уравнением  неявно. Для нахождения производной функции y (x), заданной неявно уравнением
неявно. Для нахождения производной функции y (x), заданной неявно уравнением  , достаточно продифференцировать по x обе части этого уравнения, рассматривая у как функцию от x, и из полученного уравнения выразить
, достаточно продифференцировать по x обе части этого уравнения, рассматривая у как функцию от x, и из полученного уравнения выразить 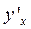 .
. задана неявно уравнением
задана неявно уравнением 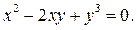
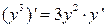 . Продифференцировав по х обе части заданного уравнения, получим:
. Продифференцировав по х обе части заданного уравнения, получим:


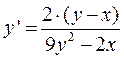 .
. .
.





 .
. принимает положительные значения. Воспользуемся логарифмической производной и свойствами логарифмов:
принимает положительные значения. Воспользуемся логарифмической производной и свойствами логарифмов:


 ,умножив обе его части на
,умножив обе его части на .
.
 .
. (1)
(1) , по формуле (1)будем получать соответствующие значения
, по формуле (1)будем получать соответствующие значения  . Можно, однако, считать у независимой переменной, а x – зависимой, задавать значения у и вычислять соответствующие им значения x. И если каждому значению у будет соответствовать единственное значение x, то равенство (1)можно рассматривать как неявное задание функции х от аргумента у. Такая функция называется обратной по отношению к данной функции у. Если уравнение (1)разрешить относительно х, получим явное выражение обратной функции, её обозначают
. Можно, однако, считать у независимой переменной, а x – зависимой, задавать значения у и вычислять соответствующие им значения x. И если каждому значению у будет соответствовать единственное значение x, то равенство (1)можно рассматривать как неявное задание функции х от аргумента у. Такая функция называется обратной по отношению к данной функции у. Если уравнение (1)разрешить относительно х, получим явное выражение обратной функции, её обозначают 
 (2)
(2) неявно.
неявно. продифференцируем уравнение (2) по у:
продифференцируем уравнение (2) по у:
 или
или  , если
, если 

 ,
,  .
. , причём
, причём  при
при 
 , получаем
, получаем  , при
, при  . Следовательно:
. Следовательно:
 , где
, где  .
. , её производная
, её производная  , для всех
, для всех  ,следовательно, функция
,следовательно, функция  .
. задаёт эту обратную функцию неявным образом. Продифференцируем обе части по х:
задаёт эту обратную функцию неявным образом. Продифференцируем обе части по х:  , откуда
, откуда  .
. выразим
выразим  , а поскольку
, а поскольку  для всех
для всех  , тополучим
, тополучим  , где
, где  .
. .
.
 .
. от функции y = y (x), заданной неявно уравнением:
от функции y = y (x), заданной неявно уравнением: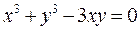






 , удовлетворяет также уравнению
, удовлетворяет также уравнению  .
.


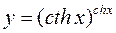


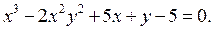




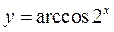

 и к графику обратной к ней функции, проходящих через точку Mo(1; 1). Сделать чертёж.
и к графику обратной к ней функции, проходящих через точку Mo(1; 1). Сделать чертёж. и к графику обратной к ней функции, проходящих через точку M0(2; 2).Сделать чертёж.
и к графику обратной к ней функции, проходящих через точку M0(2; 2).Сделать чертёж. ; 6.2.
; 6.2.  ; 6.3.
; 6.3.  ; 6.4.
; 6.4.  ; 6.5.
; 6.5.  ; 6.6.
; 6.6.  ; 6.7.
; 6.7.  ;
;





 ; 6.16.
; 6.16.  ;
; ; 6.18.
; 6.18.  ;
; ; 6.20.
; 6.20.  ; 6.21.
; 6.21. 
 ; 6.23.
; 6.23. 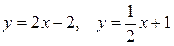 .
.


