
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия механического движенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Изменение энергии системы пропорционально работе А, совершенной внешними силами, приложенными к системе: DE = E2 – E1 = A. (72) К механической энергии относят два вида энергии – кинетическую (ЕК) и потенциальную (ЕП). Чтобы получить выражение энергии в виде функции параметров состояния механического движения, надо найти, как изменяется величина энергии с изменением величины параметров. Кинетической энергией называется энергия механической системы, зависящая от скоростей движения ее точек. Часто выделяют кинетическую энергию поступательного и вращательного движения. Для вычисления кинетической энергии подсчитаем работу, которую должна произвести результирующая сила F, чтобы тело массы m изменило скорость своего движения от V1 до V2:
– кинетическая энергия тела. Или по-другому:
Если действует еще сила трения, то Aтр < 0 и кинетическая энергия тела будет уменьшаться. Кинетическая энергия вращающегося тв`рдого тела
Кинетическая энергия твердого тела конечных размеров равна сумме кинетических энергий элементов, на которые разбито тело. Рассмотрим частный случай вращения твердого тела вокруг неподвижной оси. Кинетическая энергия каждого элемента, движущегося с линейной скоростью:
Если твердое тело одновременно участвует в двух движениях: поступательном со скоростью
Потенциальная энергия системы тел (или тела) может быть определена, если указаны взаимное расположение тел в системе и силы, действующие между ними.
Равенство (79) надо понимать алгебраически: а) если dA > 0, то потенциальная энергия уменьшается (dEП < 0); б) если dA < 0, то потенциальная энергия возрастает (dEП > 0). Учитывая, что
Это соотношение между силой и потенциальной энергией является одним из основных соотношений механики, или
Выражение а) если Сила направлена всегда в сторону уменьшения потенциальной энергии. б) производная обращается в ноль в точках, где функция достигает максимума или минимума, а это значит, что там, где потенциальная энергия имеет максимум или минимум, сила равна нулю. Изменение потенциальной энергии DЕП зависит от относительного изменения взаимного расположения взаимодействующих тел. Следовательно, потенциальная энергия U относится не только к выбранной материальной точке, но и ко всей системе и представляет собой энергию взаимодействия тел. Абсолютная величина ЕП зависит от выбора начала отсчета потенциальной энергии (где потенциальная энергия равна нулю). Обычно за начало отсчета выбирают такое положение, при котором взаимодействие практически отсутствует (когда тела удалены в бесконечность). Вычислим величину потенциальной энергии в двух случаях:
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 696; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 (73)
(73) (74)
(74) (75)
(75)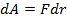 ,
,
 (76)
(76) (77)
(77) и вращательном со скоростью
и вращательном со скоростью  , то
, то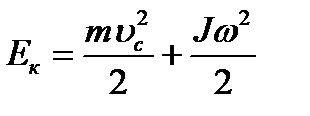 (78)
(78)
 Рис. 53. Потенциальная энергия
Рис. 53. Потенциальная энергия
 внешняя сила
внешняя сила  совершит работу
совершит работу  . При этом перемещении скорость тела не изменилась (была u = 0 и стала u = 0), значит в результате совершенной работы произошло изменение другой (некинетической) формы энергии, зависящей от координат положения тела, то есть нужно говорить о потенциальной энергии.
Обозначим через dEП – изменение потенциальной энергии при перемещении точки в силовом поле. Согласно определению работы, можно записать:
. При этом перемещении скорость тела не изменилась (была u = 0 и стала u = 0), значит в результате совершенной работы произошло изменение другой (некинетической) формы энергии, зависящей от координат положения тела, то есть нужно говорить о потенциальной энергии.
Обозначим через dEП – изменение потенциальной энергии при перемещении точки в силовом поле. Согласно определению работы, можно записать:
 . (79)
. (79) , имеем:
, имеем: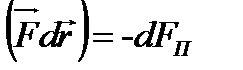 (80)
(80) . (81)
. (81) называется градиентом изменения потенциальной энергии
называется градиентом изменения потенциальной энергии  – энергия возрастает, то F будет отрицательна.
– энергия возрастает, то F будет отрицательна.


