
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Скорость и ускорение при гармоническом колебательном движении
Дифференциальное уравнение гармонических колебаний:
Решением этого дифференциального уравнения является функция
x = A sin(ωt + φ). Затухающие колебания
Все реальные собственные колебания тел являются затухающими. Потери энергии в механических системах происходят из-за ее рассеяния (например, за счет трения). Во многих случаях силы, вызывающие затухания колебаний, пропорциональны скорости:
Тогда дифференциальное уравнение колебаний примет вид:
Опыт 5.1. Колебания груза на пружине Цель работы: наблюдение вынужденных колебаний груза на пружине. Оборудование: 1. Мотор. 2. Пружины. 3. Грузики.
Рис. 86. Демонстрация опыта
Ход работы Возбуждение колебаний ведется от мотора с переменной частотой вращения через кривошипно-шатунный механизм. Имеется указатель, который показывает амплитуду и фазу возбуждающих колебаний пружины. Можно продемонстрировать явление резонанса при совпадении частот собственных колебаний пружины и частоты возбуждения системы от мотора, а также фазовые сдвиги колебаний. Наблюдаем, что при резонансе имеется фазовый сдвиг, примерно π/2.
Вывод: при высоких частотах возбуждения амплитуда резко падает, а колебания происходят примерно в противофазе с возбуждающей силой. При малых частотах – наоборот, в фазе.
Опыт 5.2. Колебания маятников Цель работы: выявить амплитудно-фазовые соотношения. Оборудование: 1. Три маятника разной длины.
Рис. 87. Колебания маятников
Ход работы
На горизонтальной планке, подвешенной на двух коротких нитях, привязаны несколько математических маятников. Один тяжелый возбуждающий колебания планки и три легких разной длины (большей, меньшей и равной длине тяжелого маятника). Наблюдения ведутся перпендикулярно плоскости качания маятник. При вынужденных колебаниях легких маятников под действием тяжелого амплитуда колебания максимальна у маятника с длиной равной длине маятника-возбудителя, а фаза его колебаний отстает примерно на π/2 от фазы колебаний маятника-возбудителя. Короткий маятник при этом колеблется почти в фазе с маятником-возбудителем, а длинный – в противофазе с возбудителем (причем амплитуды их колебаний невелики).
Вывод: максимальная амплитуда колебаний у маятника той же длины, что и маятник-возбудитель. Фаза его колебаний отстает на π/2 от фазы колебаний маятника-возбудителя. Опыт 5.3. Корыто Цель работы: изучить релаксационные колебания на примере корыта. Оборудование: 1. Корыто. 2. Вода. 3. Стойка. 4. Упругая лента.
Рис. 88. Корыто
Ход работы Одним из типов автоколебаний являются релаксационные колебания, когда энергия, поступающая в систему, периодически резко сбрасывается. 1. В демонстрируемом устройстве вода из водопровода постоянно наливается в корыто, прикрепленное сверху к горизонтальной стальной ленте, концы которой закреплены на стойках. 2. После достижения определенного уровня воды в сосуде он теряет устойчивость и опрокидывается, освобождаясь от воды. 3. Упругая лента возвращает его в исходное состояние и процесс повторяется.
Вывод: изучили релаксационные колебания на примере корыта. Опыт 5.4. Сифон Цель работы: продемонстрировать релаксационные колебания. Оборудование: 1. Цилиндр с припаянной сифонной трубкой. 2. Шланг с водой.
Рис. 89. Демонстрация опыта
Ход работы В сосуд впаяна сифонная трубка. Вода постоянно наливается в сосуд. Когда ее уровень достигает сгиба сифона, то начинается процесс быстрого слива воды из сосуда, и он опорожняется. Затем, когда вода доходит до нижнего отверстия сифонной трубки, слив прекращается и процесс повторяется вновь.
Вывод: колебания будут происходить до тех пор, пока вода будут поступать в сосуд.
Опыт 5.5. Автоколебания Цель работы: продемонстрировать один из примеров автоколебаний. Оборудование: 1. Анкерный часовой механизм.
Рис. 90. Демонстрация опыта Ход работы В качестве примера автоколебательной системы, имеющей источник энергии и устройство, регулирующее ее поступление в систему, демонстрируется анкерный часовой механизм
Вывод: автоколебания – незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счет энергии постоянного, то есть непериодического внешнего воздействия.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.180.244 (0.008 с.) |

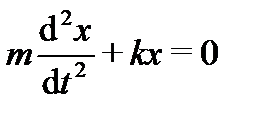 . (131)
. (131)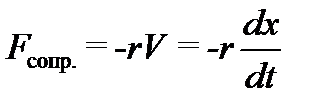 . (132)
. (132) . (133)
. (133) Рис. 85
Рис. 85
 – коэффициент затухания.
Скорость затухания колебаний определяется величиной l:
– коэффициент затухания.
Скорость затухания колебаний определяется величиной l:
 , (135)
где l – логарифмический декремент затухания (физический смысл – время, в течение которого амплитуда уменьшается в е раз).
, (135)
где l – логарифмический декремент затухания (физический смысл – время, в течение которого амплитуда уменьшается в е раз).








