Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение взаимно перпендикулярных колебаний. Фигуры лиссажу
Пусть точка М одновременно колеблется в двух взаимно перпендикулярных направлениях вдоль осей X и Y. Рассмотрим несколько случаев: 1. Составляющие колебания имеют:
ω1 = ω2 = ω,
φ1 = φ2 = 0,
А1 ≠ А2,
x = A1∙sinωt, (146)
y = A2∙sinωt. (147)
Результирующее колебание S:
2. Составляющие колебания имеют: ω1 = ω2 = ω, φ2 – φ1 = А1 ≠ А2,
3. Общий случай, когда: А1 ≠ А2,
ω1 ≠ ω2,
φ1 – φ2 = Dφ,
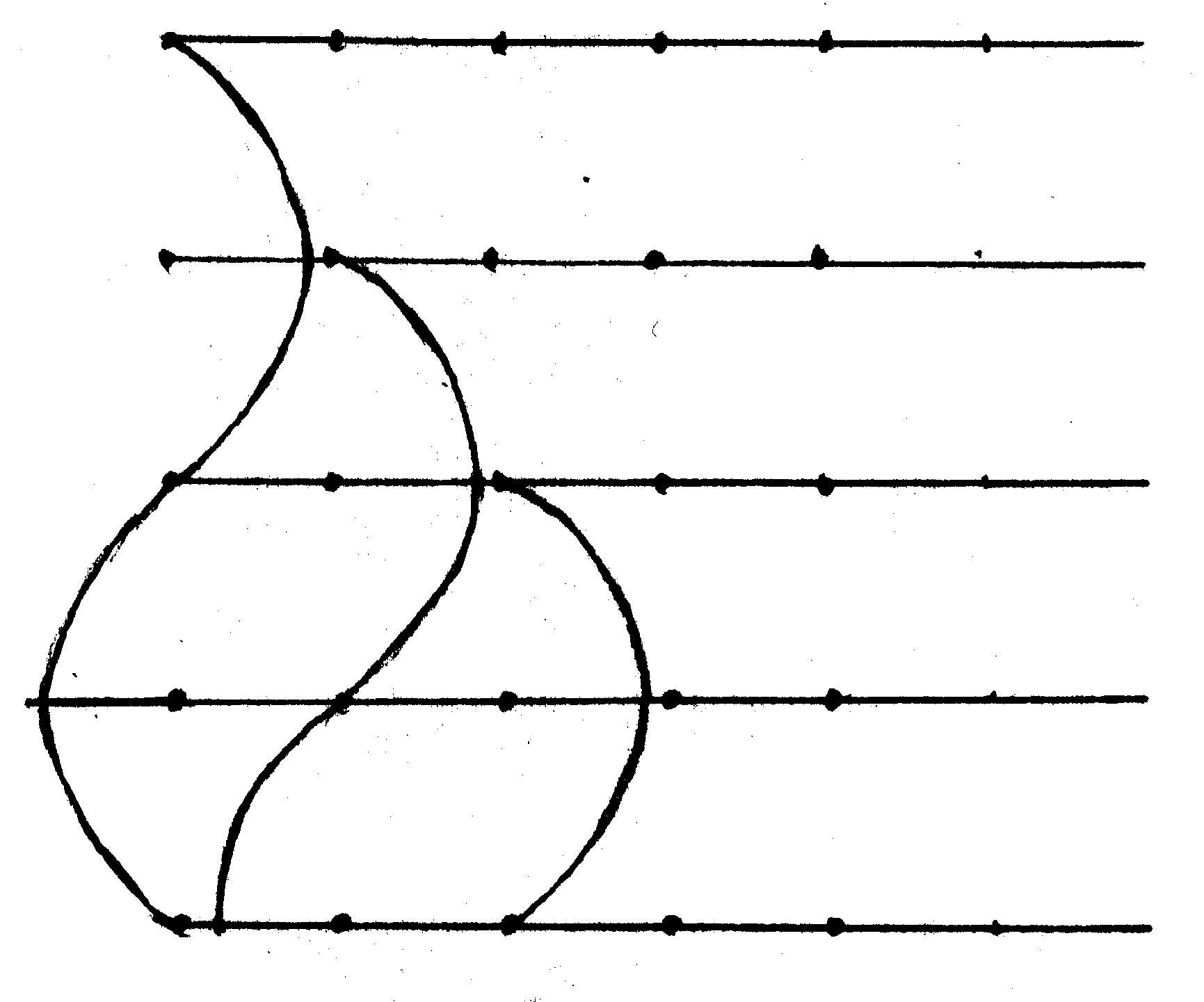
В этом случае колеблющаяся точка будет двигаться по кривым, называемым фигурами Лиссажу. Вид кривых зависит от соотношений амплитуд, частот и начальных фаз колебаний. Примеры: (А1 = А2), (φ1 = φ2).
Примеры колебательных систем 1. Пружинный маятник – тело, совершающее прямолинейные колебания (вдоль оси ОХ или ОУ) под действием упругой силы.
Рис. 102. Пружинный маятник
F = –kx, где k – коэффициент упругости.
2. Математический маятник –материальная точка, подвешенная к неподвижной точке на невесомой нерастяжимой нити (или стержне) и совершающая движение в вертикальной плоскости под действием силы тяжести:
Рис. 103. Математический маятник 3. Физический маятник – абстрактное твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси О, не проходящей через его центр тяжести С.
где Точка О1 – центр качания физического маятника. Точки О и О1 обладают свойством взаимности (взаимозаменяемости).
Вопросы к разделу 5 «Механические колебания»
1. Дайте определение колебательного процесса. 2. Какие колебания называют свободными или собственными? 3. Что называют гармоническими колебаниями? 4. Какие выводы следуют из опыта 5.1 «Колебания груза на пружине»?
5. Какие выводы следуют из опыта 5.2 «Колебания маятников»? 6. Какие выводы следуют из опыта 5.6 «Свободные колебания»? 7. Чему равна полная энергия колеблющегося тела? 8. Что называется резонансом? 9. Что называется пружинным маятником? 10. Что называется математическим маятником? 11. Что называется физическим маятником?
ВОЛНОВОЕ ДВИЖЕНИЕ
Образование волн. Поперечные и продольные волны
Процесс распространения колебаний в среде, периодический во времени и пространстве, называется волновым процессом. В механике волновой процесс происходит в среде, частицы которой связаны между собой упругими силами. Общий характер волновых процессов обычно рассматривается на примере возникновения и распространения механических волн. Волны, возникающие в среде, делятся на два типа – продольные и поперечные. Поперечные волны возникают, когда смещение колеблющихся точек направлено перпендикулярно скорости распространения волн. Продольные волны – это волны, в которых колебания частиц среды происходят вдоль направления распространения волнового процесса.
Возникновение данных видов волн зависит от упругих свойств среды, в которых распространяются волны. В твердых телах, в которых возможны упругие деформации сжатия, растяжения и сдвига, одновременно могут быть продольные и поперечные волны. В газах и жидкостях – только продольные волны, так как они не обладают упругостью в отношении сдвига.
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.102.112 (0.009 с.) |
 , (148)
– уравнение прямой через начало координат.
, (148)
– уравнение прямой через начало координат.
 .
.
 .
.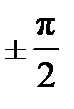 (частный случай φ1 = 0; φ2 = π/2),
(частный случай φ1 = 0; φ2 = π/2), .
. . (149)
Уравнение (145) – уравнение эллипса с полуосями А1 и А2.
Если А1 = А2, то траектория – окружность.
. (149)
Уравнение (145) – уравнение эллипса с полуосями А1 и А2.
Если А1 = А2, то траектория – окружность.
 .
. Рис. 101
Рис. 101


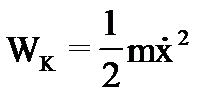 ;
; 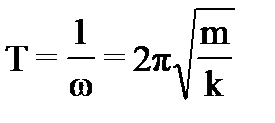 .
. .
. ,
, – приведенная длина физического маятника.
– приведенная длина физического маятника.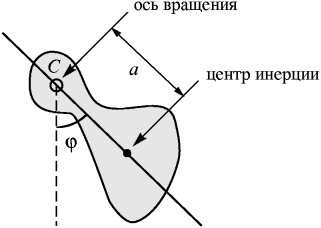 Рис. 105. Физический маятник
Рис. 105. Физический маятник


 t = T
t = T