
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диаграмма напряжений. Упругий гистерезис
Рассмотрим связь между деформацией и напряжением на графике, называемой диаграммой напряжений. (В качестве примера берется металлический образец – стержень.)
(3–3) – горизонтальная область – материал «течет». Уменьшение сечения приводит к увеличению σ (3–4) Точка 4 называется пределомпрочности. (4–5) – разрушение тела. Если область пластичности: а) большая – вязкие тела (глина); б) маленькая – хрупкие тела (стекло).
Графическая зависимость σ от ε при периодически повторяющихся деформациях, изображенная замкнутой кривой, называется петлей упругого гистерезиса. Площадь петли гистерезиса пропорциональна той части механической энергии, которая переходит во внутреннюю энергию тела за каждый цикл изменения напряжения в образце. Чем больше петля, тем сильнее нагревается тело, поэтому ответственные детали машин, подверженные периодическим нагрузкам, делают из специальных сортов стали, для которых петля гистерезиса мала.
Энергия упругой деформации
Внешняя сила, перемещая части деформированного тела, совершает работу против внутренних сил. При исчезновении деформации внутренние силы совершают работу против внешних сил. Если тело абсолютно упругое, то
Авнешних сил = Авнутренних сил.
Вычислим потенциальную энергию упругодеформированного тела, т.е. надо вычислить работу внешних сил.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 655; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.27.202 (0.005 с.) |
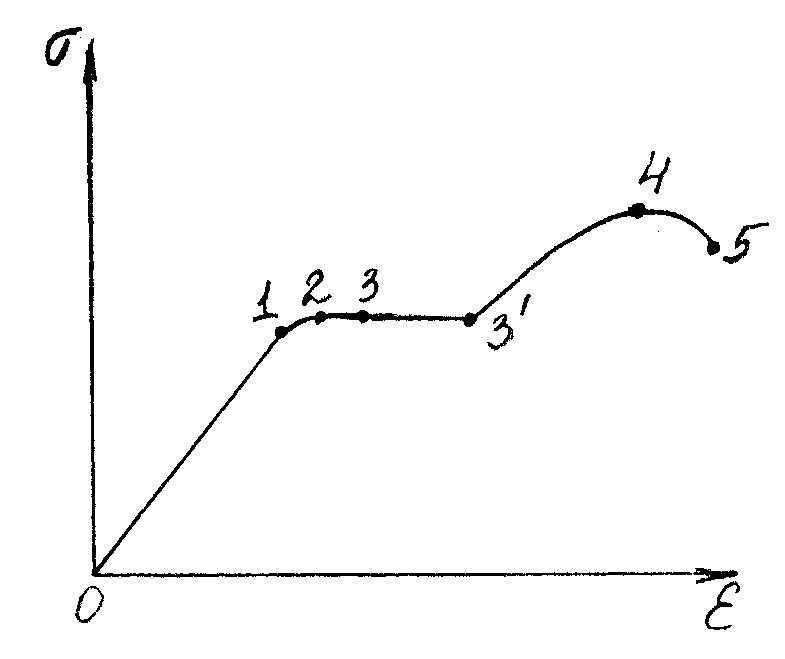 Рис. 69
Рис. 69
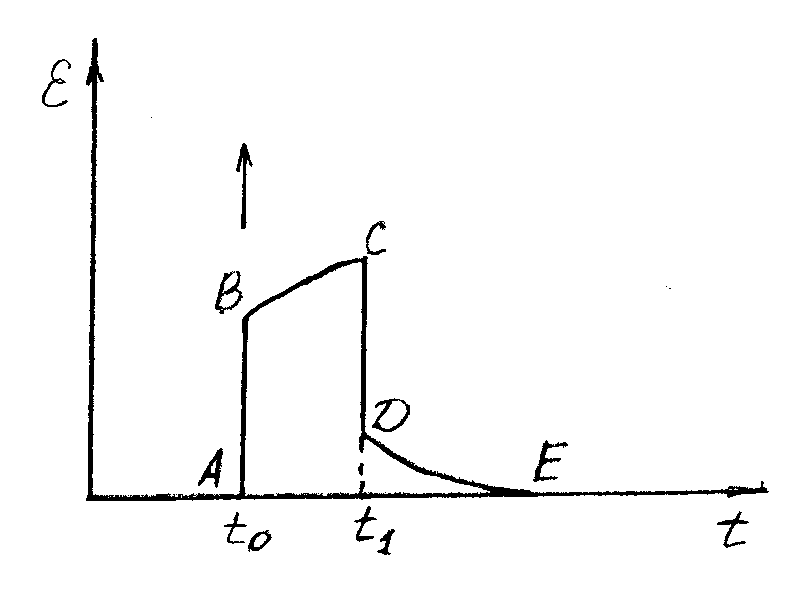 Рис. 70
Рис. 70
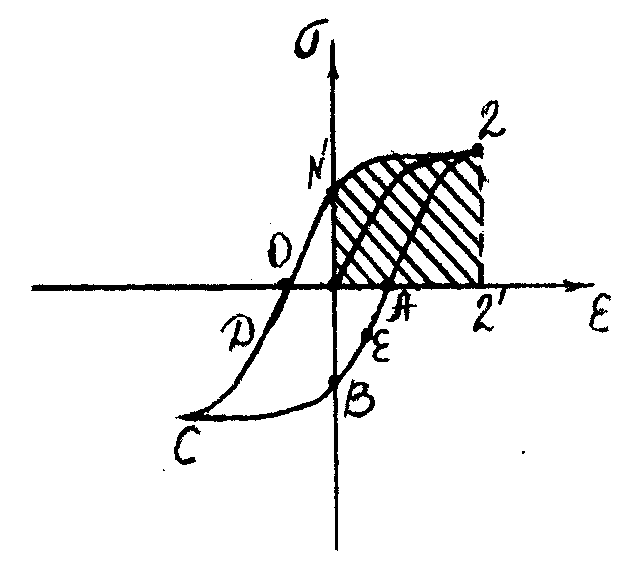 Рис. 71
Рис. 71
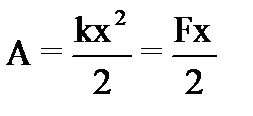 , (112)
таким образом работа А определяется площадью треугольника:
A = SD032.
, (112)
таким образом работа А определяется площадью треугольника:
A = SD032.



