
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Опыт 1.7. Сложение угловых скоростей
Цель работы: провести опыт для изучения сложения угловых скоростей на примере шара с точками. Оборудование: 1. Шар с точками.
Рис. 21. Демонстрация опыта
Ход работы Черный шар с белыми точками может приводиться в независимое вращение вокруг двух взаимно перпендикулярных осей – вертикальной и горизонтальной. Угловые скорости вращения вокруг каждой из осей регулируются от нуля до некоторой максимальной величины. Сложное движение твердого тела, то есть вращение одновременно вокруг двух осей, сводится к вращению вокруг мгновенной оси, которая движется и в пространстве и относительно тела. Вблизи мгновенной оси смазывание белых точек на черном шаре минимально, так как их скорости близки к нулю. Из-за перемещения мгновенной оси вращения легко следить по перемещению этих несмазанных точек: 1. Сначала мы раскрутили шар вокруг одной оси. 2. Затем постепенно увеличиваем скорость его движения вокруг второй оси, а первую скорость будем уменьшать. При этом мгновенная ось вращения пройдет все положения, от горизонтального до вертикального. 3. Затем опыт повторим в обратном порядке от вертикали до горизонтали. Особенно хорошо несмазанные точки видны при замедленном воспроизведении опыта. Вначале шар раскручен вокруг вертикальной оси, затем мы постепенно добавляем горизонтальную скорость вращения, а вертикальную уменьшаем и видим, как эти несмазанные точки постепенно перемещаются от вертикального диаметра шара к горизонтальному. При этом заметно, что шар не крутится вокруг одной какой-то точки, а эти точки постоянно меняются, то есть то не крутиться одна, то другая. То есть мгновенная ось вращения движется и относительно тела также.
Вывод: провели опыт с шаром с точками. Рассмотрели сложения угловых скоростей на примере этого шара.
При неравномерном вращения выражения для мгновенных значений ω и ε имеют вид:
где ε – угловое ускорение. Каждая точка твердого тела (например, точка А) движется по окружности радиуса r с линейной скоростью DS = RDφ, (35)
или dS = Rdφ, (36)
но
и
Дополнительные данные о вращательном движении: а) каждая точка твердого тела обладает нормальным ускорением an; б) полное ускорение:
в) связь частоты ν и периода Т:
г) Поскольку взаимное расположение элементов (точек) твердого тела не изменяется, для изучения его достаточно изучить движение одной его точки. Точка, движение которой эквивалентно движению твердого тела, массой М под действием результирующей внешних сил F, называется центр масс тела (центр инерции).
Вопросы к разделу 1 «Кинематика»
1. Дайте определение материальной точке. 2. Охарактеризуйте виды движения в зависимости от формы траектории. 3. Что называется вектором перемещения? 4. Перечислите оборудование для опыта 1.1 «Равномерное движение». 5. Перечислите оборудование для опыта 1.4 «Падение тел». Какой вывод следует из этого опыта? 6. Дайте определение мгновенной скорости. 7. По какой формуле можно найти путь, пройденный телом за промежуток времени ∆t? 8. Что называется ускорением? 9. Напишите формулы для вычисления среднего и мгновенного ускорений. 10. Какие системы отсчета называются инерциальными? 11. Сформулируйте принцип относительности Галилея. 12. Что называется твердым телом? 13. Какое движение называют поступательным? 14. Какое движение называют вращательным? 15. Какие выводы следуют из опыта с точилом? 16. Запишите формулы для вычисления угловой скорости, углового ускорения. 17. Запишите формулу, связывающую угловую и линейную скорости, угловое и тангенциальное ускорения. 18. Запишите формулу для вычисления полного ускорения. 19. Запишите формулу, связывающую частоту и период вращения.
20. Что называется центром масс тела?
ДИНАМИКА
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 585; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.161.77 (0.01 с.) |

 Рис. 22. Вращение твердого тела вокруг неподвижной оси
Рис. 22. Вращение твердого тела вокруг неподвижной оси
 , (32)
где ωср – средняя угловая скорость тела.
Угловая скорость – вектор, имеющий направление правого винта и направлен по оси вращения.
, (32)
где ωср – средняя угловая скорость тела.
Угловая скорость – вектор, имеющий направление правого винта и направлен по оси вращения.
 (33)
(33)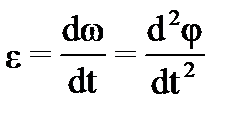 , (34)
, (34) . Тогда за время Dt тело переместится на:
. Тогда за время Dt тело переместится на: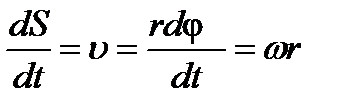 , (37)
, (37) (38)
(38) , (39)
, (39) . (40)
. (40) ; (41)
; (41) ; (42)
; (42) . (43)
. (43)


